Chapter 4 Pure Premium
4.1 Introduction
The pure premium represents the price of risk: it is the amount that the insurer must have to compensate (on average) policyholders for incurred claims, without surplus or deficit. The total pure premiums related to the portfolio must enable the insurer to fulfill its guarantee obligations. If the insurer wishes to retain profits (for example, to compensate shareholders or increase its capital), these will be added later. Hence, the pure premium is expected to be entirely used to compensate claims affecting policyholders: the entirety of the pure premium collected will thus be returned to policyholders in the form of indemnities.
The pure premium is calculated by considering various factors: the probability of occurrence or frequency of claims, the extent of losses, the insured amount, etc. In this work, we focus on insurance products with short-term and high-risk risks. This leads us to not explicitly model financial products, a simplification that has no consequence. This contrasts significantly with long-term and low-risk actuarial practices that characterize life insurance products. In such cases, explicit modeling of financial products is essential. In non-life insurance, neglecting financial products provides actuaries with an implicit safety margin.
The central concept justifying the existence of an insurance market is risk aversion or “risk-aversion.” This is the natural tendency of economic agents to avoid risk and protect themselves from the negative consequences of unforeseeable events. Of course, not everyone shares this sentiment, and those who do share it do not all do so to the same extent.
The formalization of the concept of risk aversion is quite difficult due to the diversity of human behavior. However, the concept of pure premium developed in this chapter allows for the objectification of risk aversion: an economic agent will now be considered risk-averse when they transfer all their risks to an insurer who charges them the pure premium. As we will see in the next chapter, the insurer is obliged to charge the insured a premium (sometimes significantly higher than the pure premium), which will explain a partial transfer of risks, even by risk-averse individuals.
Remark. An economic agent is therefore considered risk-averse when faced with a choice between a random financial flow and a deterministic flow with the same mean, they will always prefer the latter. Thus, such a decision-maker will always prefer to receive €1 over the result of a coin toss game where they would win €2 if heads is obtained, and nothing otherwise. This formalization of risk aversion certainly has the advantage of objectivity and simplicity but unfortunately lacks subtlety. Indeed, many rational economic agents (meaning those with a correct perception of the risks they are exposed to and who protect themselves accordingly) buy lottery tickets (i.e., replace a deterministic amount, the price of the lottery ticket, with a random gain with a lower average). Thus, some of our readers might agree to play the coin toss game as described above, even if they are convinced of the utility of insurance contracts. It is therefore not uncommon for an individual to exhibit risk aversion only beyond a certain financial threshold and occasionally engage in irrational behavior below that threshold. If, in the above example, €1,000,000 is at stake, most readers will undoubtedly prefer to keep that million rather than risking it on a coin toss.
4.3 Variance
4.3.1 Definition
Variance measures the spread of possible values for a random variable around its mean. It is defined as follows.
Definition 4.1 The variance of the random variable \(X\), denoted \(\mathbb{V}[X]\), is the second moment of this centered variable, i.e., \[ \mathbb{V}[X]=\mathbb{E}[(X-\mathbb{E}[X])^2]. \]
It is, therefore, an average of the squared deviations \(x-\mathbb{E}[X]\) between the realization \(x\) of \(X\) and its expected value \(\mathbb{E}[X]\). The variance of \(X\) can also be expressed as \[\begin{eqnarray*} \mathbb{V}[X]&=&\mathbb{E}\big[X^2-2\mathbb{E}[X]X+\{\mathbb{E}[X]\}^2\big]\\ &=&\mathbb{E}[X^2]-\{\mathbb{E}[X]\}^2. \end{eqnarray*}\] Thus, the variance of \(X\) is the expectation of the squared variable, subtracting the square of the expectation.
In the following, we will use the standard deviation of the random variables in question extensively, the definition of which is given below.
Definition 4.2 The positive square root of the variance is called the standard deviation.
4.3.2 Actuarial Interpretation
Note that the variance has a clear interpretation in terms of the distance \(d_2\) introduced earlier to determine the pure premium for a risk \(S\), as \(d_2(S,\mathbb{E}[S])=\mathbb{V}[S]\). So, the variance becomes very important here, as it measures the distance between the random expenses \(S\) of the insurer and the pure premium \(\mathbb{E}[S]\) that it will charge the insured. Thus, it’s a measure of the risk the insurer takes in replacing \(S\) with \(\mathbb{E}[S]\) (in terms of the distance \(d_2\)).
4.3.3 Some Examples
The significance of variance in probability and statistics also stems from its special role in the normal distribution.
Example 4.9 (Variance associated with the Standard Normal Distribution) Let’s start with \(Z\sim\mathcal{N}or(0,1)\). Since \(\mathbb{E}[Z]=0\), \[ \mathbb{V}[Z]=\mathbb{E}[Z^2]=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{+\infty}x^2\exp(-x^2/2)dx \] which, by integrating by parts, gives \[\begin{eqnarray*} \mathbb{V}[Z]&=&-\frac{1}{\sqrt{2\pi}}\Big[x\exp(-x^2/2)\Big]_{-\infty}^{+\infty}\\ &&+\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{+\infty}\exp(-x^2/2)dx=1. \end{eqnarray*}\]
Example 4.10 (Variance associated with the Poisson Distribution) When \(N\sim\mathcal{P}oi(\lambda)\), \[\begin{eqnarray*} \mathbb{E}[N^2] & = & \sum_{k=1}^{+\infty}k^2\exp(-\lambda)\frac{\lambda^k}{k!} \nonumber\\ & = & \exp(-\lambda)\sum_{k=0}^{+\infty}(k+1)\frac{\lambda^{k+1}}{k!} =\lambda+\lambda^2,\tag{4.6} \end{eqnarray*}\] so that \[ \mathbb{V}[N]=\mathbb{E}[N^2]-\lambda^2=\lambda. \] Returning to Example 4.2, we observe that the Poisson distribution stands out because \[ \mathbb{E}[N]=\mathbb{V}[N]=\lambda, \] thus reflecting equidispersion and significantly limiting its applicability, as the sample mean and variance are often quite different.
Remark. Not all random variables have finite variance. It is possible for a variable to have a finite mean (indicating insurability from an actuarial perspective), but an infinite variance, indicating significant risk for the insurer. This is the case for Pareto distributions with a tail index between 1 and 2. For instance, consider \(X\sim\mathcal{P}ar(\alpha,\theta)\) with \(\alpha>2\). Then, \[\begin{eqnarray*} \mathbb{E}[X^2] & = & \int_{x=0}^{+\infty}x^2\frac{\alpha\theta^\alpha}{(x+\theta)^{\alpha+1}}dx \\ & = & -\left[\frac{x^2\theta^\alpha}{(x+\theta)^\alpha}\right]_{x=0}^{+\infty} +\int_{x=0}^{+\infty}2x\frac{\theta^\alpha}{(x+\theta)^{\alpha}}dx \\ & = & \left[\frac{2x\theta^\alpha}{(x+\theta)^{\alpha-1}(-\alpha+1)}\right]_{x=0}^{+\infty}\\ & & +\int_{x=0}^{+\infty}2\frac{\theta^\alpha}{(\alpha-1)(x+\theta)^{\alpha-1}}dx \\ & = & \frac{2\theta^2}{(\alpha-1)(\alpha-2)}. \end{eqnarray*}\] If \(\alpha<2\), then \(\mathbb{E}[X^2]=+\infty\). Therefore, if \(2>\alpha>1\), \[ \mathbb{E}[X]=\frac{\theta}{\alpha-1}<+\infty\text{ and }\mathbb{V}[X]=+\infty. \]
4.3.4 Properties
4.3.4.1 Invariance under Translation
Note that \[ \mathbb{V}[S]=\mathbb{V}[S+c] \] for any real constant \(c\). This reflects the intuitive idea that adding a real constant \(c\) to a risk \(X\) doesn’t make the insurer’s situation more dangerous. The insurer can simply charge a premium of \(\mathbb{E}[S]+c\) instead of \(\mathbb{E}[S]\).
4.3.4.2 Change of Scale
For any constant \(c\), it’s easy to see that \[ \mathbb{V}[cS]=c^2\mathbb{V}[S], \] so the variance is affected by a change in measurement units (for example, switching from euros to thousands of euros). This is why the coefficient of variation (see below) is introduced.
::: {.example name = “Variance associated with the Normal Distribution”} For \(X\sim\mathcal{N}or(\mu,\sigma^2)\), we know that \(X=_{\text{dist}}\mu+\sigma Z\) where \(Z\sim\mathcal{N}or(0,1)\), so according to Example 4.9, \[ \mathbb{V}[X]=\mathbb{V}[\mu+\sigma Z]=\sigma^2. \] Hence, the second parameter of the normal distribution is its variance. :::
4.3.4.3 Additivity for Independent Risks
The following result shows how the variance of a sum of independent random variables decomposes.
Proposition 4.5 (Variance of a Sum of Independent Variables) If the random variables \(X_1,X_2,\ldots,X_n\) are independent, then \[ \mathbb{V}\left[\sum_{i=1}^nX_i\right]=\sum_{i=1}^n\mathbb{V}[X_i]. \]
Proof. It’s sufficient to write \[\begin{eqnarray*} \mathbb{V}\left[\sum_{i=1}^nX_i\right]&=&\mathbb{E}\left[\left(\sum_{i=1}^n(X_i-\mathbb{E}[X_i])\right)^2\right]\\ &=&\mathbb{E}\left[\left(\sum_{i=1}^n(X_i-\mathbb{E}[X_i])\right)\left(\sum_{j=1}^n(X_j-\mathbb{E}[X_j])\right)\right]\\ &=&\sum_{i\neq j}\mathbb{E}\big[X_i-\mathbb{E}[X_i]\big]\mathbb{E}\big[X_j-\mathbb{E}[X_j]\big] +\sum_{i=1}^n\mathbb{E}\big[\big(X_i-\mathbb{E}[X_i]\big)^2\big]\\ &=&\sum_{i=1}^n\mathbb{V}[X_i]. \end{eqnarray*}\]
Thus, the variance of a sum of independent random variables is the sum of the variances of each of them.
Example 4.11 (Variance associated with the Binomial Distribution) When \(N\sim\mathcal{B}in(m,q)\), \(N=_{\text{dist}}N_1+\ldots+N_m\) where the \(N_i\) are independent with distribution \(\mathcal{B}er(q)\). Property 4.5 then gives \[ \mathbb{V}[N]=\sum_{k=1}^m\mathbb{V}[N_k]=mq(1-q). \] So, the binomial distribution exhibits under-dispersion of data, as \(\mathbb{V}[N]<\mathbb{E}[N]=mq\).
4.3.5 Variance of Common Distributions
The variances associated with common probability distributions are shown in Table 4.2. If we consider variance as a risk criterion, this table allows us to assess how the parameters influence the risk associated with the number or cost of losses.
| Probability Law | Variance |
|---|---|
| \(\mathcal{DU}ni(n)\) | \(\frac{n^2+n}{12}\) |
| \(\mathcal{B}er(q)\) | \(q(1-q)\) |
| \(\mathcal{B}in(m,q)\) | \(mq(1-q)\) |
| \(\mathcal{G}eo(q)\) | \(\frac{1-q}{q^2}\) |
| \(\mathcal{NB}in(\alpha,q)\) | \(\frac{\alpha(1-q)}{q^2}\) |
| \(\mathcal{P}oi(\lambda)\) | \(\lambda\) |
| Probability Law | Variance |
|---|---|
| \(\mathcal{N}or(\mu,\sigma^2)\) | \(\sigma^2\) |
| \(\mathcal{LN}or(\mu,\sigma^2)\) | \(\exp(2\mu+\sigma^2)(\exp(\sigma^2)-1)\) |
| \(\mathcal{E}xp(\theta)\) | \(\frac{1}{\theta^2}\) |
| \(\mathcal{Gam}(\alpha,\tau)\) | \(\frac{\alpha}{\tau^2}\) |
| \(\mathcal{Par}(\alpha,\theta)\) | \(\frac{\alpha\theta^2}{(\alpha-2)(\alpha-1)^2}\) if \(\alpha>2\) |
| \(\mathcal{Bet}(\alpha,\beta)\) | \(\frac{\alpha\beta}{(\alpha+\beta+1)(\alpha+\beta)^2}\) |
| \(\mathcal{U}ni(a,b)\) | \(\frac{(b-a)^2}{12}\) |
4.3.6 Variance of Composite Distributions
Let’s now turn our attention to the variance of composite distributions. The following result indicates how the variance of a composite distribution can be decomposed in terms of the variance of the number of terms and the variance of each term.
Proposition 4.6 If \(S\) is of the form (??), i.e., \(S=\sum_{i=1}^NX_i\) where \(X_i\), \(i=1,2,\ldots\), are independent and identically distributed, and independent of \(N\), then its variance is given by \[\begin{eqnarray*} \mathbb{V}[S] &=&\mathbb{E}[N]\mathbb{V}[X_1]+\mathbb{V}[N]\mathbb{E}^2[X_1]. \end{eqnarray*}\]
Proof. This comes from \[\begin{eqnarray*} \mathbb{E}[S^2]&=&\mathbb{E}\left[\sum_{i=1}^N\sum_{j=1}^NX_iX_j\right]\\ &=&\mathbb{E}\left[\sum_{i=1}^NX_i^2\right]+\mathbb{E}\left[\sum_{i\neq j}^NX_iX_j\right]\\ &=&\mathbb{E}[N]\mathbb{E}[X_1^2]+\big(\mathbb{E}[X_1]\big)^2\big(\mathbb{E}[N^2]-\mathbb{E}[N]\big), \end{eqnarray*}\] which gives the announced result after grouping terms.
We can interpret this decomposition of variance as follows. The first term can be thought of as \(\mathbb{V}[\sum_{i=1}^{\mathbb{E}[N]}X_i]\) by considering momentarily \(\mathbb{E}[N]\) as an integer. Thus, it represents the portion of the variance of \(S\) attributed solely to the variability in the costs of losses \(X_1,X_2,\ldots\). The second term in the variance decomposition of \(S\) can be viewed as \(\mathbb{V}[\sum_{i=1}^N\mathbb{E}[X_i]]\), i.e., the part of the variability in \(S\) due to the variability in the number of losses, with their costs fixed at their mean value.
Example 4.12 Several interesting special cases can be derived easily from Tables 4.1 and 4.2. If \(N\sim\mathcal{B}in(m,q)\), then \[ \mathbb{V}[S]=mq\Big(\mathbb{E}[X_1^2]-q\big(\mathbb{E}[X_1]\big)^2\Big). \] If \(N\sim\mathcal{P}oi(\lambda)\), then \[ \mathbb{V}[S]=\lambda\mathbb{V}[X_1]+\lambda\mathbb{E}^2[X_1]=\lambda \mathbb{E}[X_1^2]. \]
4.3.7 Coefficient of Variation and Risk Pooling
The coefficient of variation is defined as the ratio of the standard deviation to the mean, i.e., \[ CV[X]=\frac{\sqrt{\mathbb{V}[X]}}{\mathbb{E}[X]}. \] The coefficient of variation has the significant advantage of being a dimensionless number, which facilitates comparisons (excluding, for instance, the effects of different monetary units). It can be seen as a normalization of the standard deviation.
The coefficient of variation plays a particularly important role in actuarial science. It can be interpreted as the standard deviation of the “losses over pure premiums” ratio, traditionally denoted as L/P.
4.4 Insurance and Bienaymé-Chebyshev Inequality
4.4.1 Markov’s Inequality
Here we present one of the most famous inequalities in probability theory.
Proposition 4.7 (Markov's Inequality) Given a random variable \(X\), any non-negative function \(g:{\mathbb{R}}\to{\mathbb{R}}^+\), and a constant \(a>0\), we have \[ \Pr[g(X)> a]<\frac{\mathbb{E}[g(X)]}{a}. \]
Proof. The inequality \[ g(X)> a\mathbb{I}[g(X)> a], \] yields, by taking the expectation, \[ \mathbb{E}[g(X)]> a\Pr[g(X)> a], \] which gives the desired result.
4.4.2 Bienaymé-Chebyshev Inequality
The Bienaymé-Chebyshev inequality controls the deviation between a random variable and its mean. It is derived as a straightforward consequence of Markov’s inequality.
Proposition 4.8 (Bienaymé-Chebyshev Inequality) Given a random variable \(X\) with mean \(\mu\) and finite variance \(\sigma^2\), we have \[ \Pr\big[|X-\mu|>\epsilon\big]<\frac{\sigma^2}{\epsilon^2} \] for any \(\epsilon>0\).
Proof. Just apply Markov’s inequality to \(g(x)=(x-\mu)^2\) and \(a=\epsilon^2\).
4.4.3 Actuarial Interpretation of the Bienaymé-Chebyshev Inequality
As we discussed earlier, variance (and therefore standard deviation) measures the distance between the financial burden \(S\) of the insurer and the corresponding pure premium \(\mu=\mathbb{E}[S]\). Therefore, we might wonder what we can say about the gap between \(S\) and its mean using the knowledge of variance. The Bienaymé-Chebyshev inequality tells us that \[\begin{equation} \Pr\Big[|S-\mu|\leq t\sigma\Big]>1-\frac{1}{t^2} \Leftrightarrow \Pr\Big[|S-\mu|>t\sigma\Big]<\frac{1}{t^2} \tag{4.7} \end{equation}\] for any \(t>0\).
The inequalities (4.7) are of interest only if \(t>1\). They imply that a random variable \(S\) with finite variance cannot deviate “too much” from its mean \(\mu\), and they are of considerable importance to actuaries (interpreting \(S\) as a loss amount and \(\mu\) as the corresponding pure premium). Thus, the probability that the loss amount \(S\) deviates from the pure premium \(\mu\) by \(t=10\) times the standard deviation \(\sigma\) is always less than \(1/t^2=1\%\).
4.4.4 Conservative Nature of the Bienaymé-Chebyshev Inequality
Before moving forward, it’s important to note that the Bienaymé-Chebyshev inequality holds in a very general sense, so the upper bound it provides is often very (or overly) conservative. For illustration, in Figure 4.1, we have plotted the function \[\begin{equation} t\mapsto\frac{1/t^2}{\Pr\big[|\mathcal{G}am(1/2,1/2)-1|>t\sqrt{2}\big]}, \tag{4.8} \end{equation}\] which is the ratio between the upper bound provided by the Bienaymé-Chebyshev inequality and the probability that a Gamma-distributed variable with mean 1 and variance 2 deviates from its mean by more than \(t\) times the standard deviation. It’s evident that the upper bound \(1/t^2\) is significantly above the exact value in this case. Figure 4.1 also provides similar results for the log-normal distribution with the same mean and variance, given by the function \[\begin{equation} t\mapsto\frac{1/t^2}{\Pr\big[|\mathcal{LN}or(\mu,\sigma^2)-1|>t\sqrt{2}\big]}, \tag{4.9} \end{equation}\] where \[ \mu=-\frac{\ln 3}{2}\mbox{ and }\sigma^2=\ln 3, \] and for the Pareto distribution with the same first two moments, i.e., \[\begin{equation} t\mapsto\frac{1/t^2}{\Pr\big[|\mathcal{P}ar(\alpha,\theta)-1|>t\sqrt{2}\big]}, \tag{4.10} \end{equation}\] where \[ \alpha=4\mbox{ and }\theta=3. \]
It’s clear that the upper bound provided by (4.7) is very cautious.
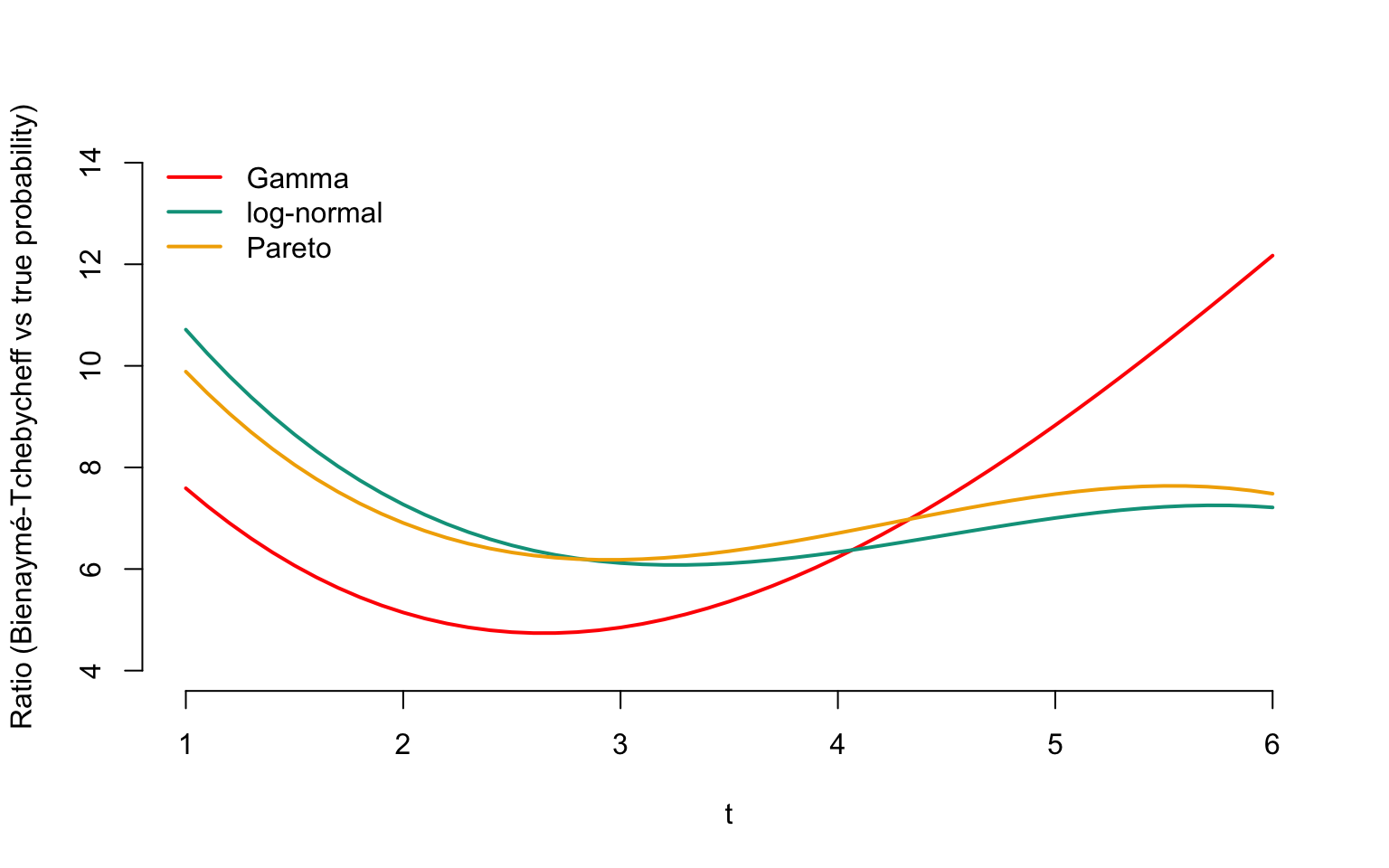
Figure 4.1: Evoluation of ratios between Bienaymé-Tchebycheff upper bound and the true probability
4.5 Insurance and Law of Large Numbers
4.5.1 Convergence in Probability
The law of large numbers provides a relevant justification for the calculation method of the pure premium associated with \(S\). To understand this, we need a concept of convergence for a sequence of random variables.
Definition 4.3 The sequence \(\{T_n,\hspace{2mm}n\in{\mathbb{N}}\}\) converges in probability to the random variable \(T\), denoted as \[ T_n\to_{\text{proba}}T, \] when \[ \Pr\big[|T_n-T|>\epsilon\big]\to 0\mbox{ as }n\to +\infty \] for any \(\epsilon>0\).
This expresses the fact that as \(n\) increases, the probability that \(T_n\) deviates from its limit \(T\) by more than \(\epsilon\) tends towards 0; \(T_n\) gets closer to its limit \(T\) as \(n\) gets larger.
4.5.3 Case of Flat Indemnity
4.5.3.1 At Most One Claim per Period
Let’s assume the insurer covers \(n\) individuals. In the event of a claim, the company is obligated to pay a flat amount \(s\). Each policy results in at most one claim. The random variable \(S_i\) representing the company’s reimbursement to individual \(i\) is given by \[\begin{equation} S_i=\left\{ \begin{array}{l} 0,\text{ with probability }1-q, \\ s,\text{ with probability }q. \end{array} \right.\tag{4.12} \end{equation}\] If the \(S_i\) are independent, then \[ \overline{S}^{(n)}\to_{\text{proba}}\mathbb{E}[S_1]=qs. \] The difference between \(\overline{S}^{(n)}\) and the pure premium \(qs\) is bounded using the Bienaymé-Chebyshev inequality by \[ \Pr\Big[|\overline{S}^{(n)}-qs|>\epsilon\Big]\leq\frac{1}{n\epsilon^2}s^2q(1-q). \]
4.5.3.2 Random Number of Claims per Period
If the policy can generate more than one claim per period, and the occurrence of any of these claims obligates the insurer to pay \(s\), the company’s expenditure is given by \(S_i=sN_i\), where \(N_i\) is the number of claims reported by policy \(i\).
In this case, \[ \overline{S}^{(n)}=s\overline{N}^{(n)}\text{ where }\overline{N}^{(n)}=\frac{1}{n}\sum_{i=1}^nN_i \text{ and }\overline{S}^{(n)}\to_{\text{proba}} s\mathbb{E}[N_1]. \] The difference between \(\overline{S}^{(n)}\) and the pure premium is controlled by \[ \Pr\Big[|\overline{S}^{(n)}-s\mathbb{E}[N_1]|>\epsilon\Big]\leq\frac{1}{n\epsilon^2}s^2\mathbb{V}[N_1]. \]
4.5.4 Case of Indemnity Compensation
4.5.4.1 Without Considering the Number of Claims
Now, suppose there’s a probability \(q\) that \(S_i>0\), and let \(Z_i\) be the amount of the claims when \(S_i>0\), i.e. \[\begin{equation} S_i=\left\{ \begin{array}{l} 0,\text{ with probability }1-q, \\ Z_i,\text{ with probability }q, \end{array} \right.\tag{4.13} \end{equation}\] where \(Z_1,Z_2,\ldots\) are positive, independent, and identically distributed random variables. In this case, the pure premium will be \(\mathbb{E}[S_i]=q\mathbb{E}[Z_i]=q\mu\).
We can represent \(S_i\) as \(J_iZ_i\) where \(J_i=\mathbb{I}[S_i>0]\). This time, the difference between \(\overline{S}^{(n)}\) and the pure premium \(q\mu\) is bounded using the Bienaymé-Chebyshev inequality by \[\begin{eqnarray*} \Pr\Big[|\overline{S}^{(n)}-q\mu|>\epsilon\Big]&\leq&\frac{1}{n\epsilon^2}\mathbb{V}[S_1]\\ &=&\frac{1}{n\epsilon^2}\big(q\sigma^2+\mu^2q(1-q)\big), \end{eqnarray*}\] where \(\sigma^2=\mathbb{V}[Z_1]\).
Remark. In some cases, it might be useful for the actuary to explicitly include the number of claims made by the insured. In this case, the model could be represented as \[ S_i=\sum_{k=1}^{N_i}C_{ik}. \] The pure premium would then be \[ \mathbb{E}[S_i]=\mathbb{E}[N_i]\mathbb{E}[C_{i1}]. \]
4.6 Characteristic Functions
4.6.1 Probability Generating Function
4.6.1.1 Definition
The probability generating function is a convenient tool for obtaining a series of valuable results for actuaries, although it lacks an intuitive interpretation. It is defined as follows.
Definition 4.4 The probability generating function of a random variable \(N\) taking values in \(\mathbb{N}\), denoted by \(\varphi_N\), is defined as \[ \varphi_N(z)=\mathbb{E}[z^N]=\sum_{j\in\mathbb{N}}\Pr[N=j]z^j, \quad 0\leq z\leq 1. \]
This function characterizes the probability distribution of \(N\). In fact, the successive derivatives of \(\varphi_N\) evaluated at \(z=0\) provide the probabilities \(\Pr[N=k]\) with a factor, i.e., \[\begin{eqnarray*} \Pr[N=0]&=&\varphi_N(0),\\ k!\Pr[N=k] &=& \left.\frac{d^k}{dz^k}\varphi_N(z)\right|_{z=0}, \quad k\geq 1. \end{eqnarray*}\] The successive derivatives of \(\varphi_N\) evaluated at \(z=1\) provide the factorial moments, namely \[\begin{eqnarray*} \left.\frac{d}{dz}\varphi_N(z)\right|_{z=1} & = & \mathbb{E}[N],\\ \left.\frac{d^k}{dz^k}\varphi_N(z)\right|_{z=1} &=& \mathbb{E}[N(N-1)\ldots(N-k+1)], \quad k\geq 1. \end{eqnarray*}\] Note that, obviously, \(\varphi_N(1)=1\).
The probability generating functions associated with the common discrete probability distributions are listed in Table 4.3.
| Probability Law | Probability Generating Function |
|---|---|
| \(\mathcal{DU}ni(n)\) | \(\frac{1}{n+1}\frac{t^{n+1}-1}{t - 1}\) |
| \(\mathcal{B}er(q)\) | \((1-q + q t)\) |
| \(\mathcal{B}in(m,q)\) | \((1-q +qt)^m\) |
| \(\mathcal{G}eo(q)\) | \(\frac{q}{1-(1-q)t}\) |
| \(\mathcal{NB}in(\alpha,q)\) | \(\left( \frac{q}{1-(1-q)t} \right) ^\alpha\) |
| \(\mathcal{P}oi(\lambda)\) | \(\exp( \lambda (t -1))\) |
4.6.1.2 Probability Generating Function and Convolution
The main advantage of the probability generating function lies in its easy handling of convolutions. If we want to find the probability generating function of a sum of independent counting variables, we only need to multiply the probability generating functions of each term, as shown by the following result.
Proposition 4.10 The probability generating function of \(N_\bullet=\sum_{i=1}^nN_i\), where the \(N_i\) are independent, is given by the product of the generating functions \(\varphi_{N_i}\) of each term.
Proof. We just need to write \[\begin{eqnarray*} \varphi_{N_\bullet}(z) & = & \mathbb{E}\left[z^{\sum_{i=1}^nN_i}\right]=\mathbb{E}\left[\prod_{i=1}^n z^{N_i}\right] \\ & = & \prod_{i=1}^n\mathbb{E}[z^{N_i}]=\prod_{i=1}^n\varphi_{N_i}(z),\quad z\in[0,1]. \end{eqnarray*}\]
In particular, if \(N_1,\ldots,N_n\) are independent and identically distributed, we have \[ \varphi_{N_\bullet}(z)=\{\varphi_{N_1}(z)\}^n. \]
Example 4.13 (Convolution of Binomial Distributions with Same Parameter) Let’s consider two independent random variables \(N_1\) and \(N_2\) with distributions \(\mathcal{B}in(m_1,q)\) and \(\mathcal{B}in(m_2,q)\) respectively. The probability generating function of the sum \(N_1+N_2\) is given by \[ \varphi_{N_1+N_2}(z)=\varphi_{N_1}(z)\varphi_{N_2}(z)=\big(1+q(z-1)\big)^{m_1+m_2}, \] which shows that \(N_1+N_2\sim\mathcal{B}in(m_1+m_2,q)\). Therefore, the Bernoulli distribution provides the foundation for the binomial family, as any random variable \(N\) with a \(\mathcal{B}in(m,q)\) distribution can be represented as \[ N=\sum_{i=1}^mN_i, \] where the \(N_i\) are independent and follow a \(\mathcal{B}er(q)\) distribution.
Example 4.14 (Convolution of Poisson Distributions) Let \(N_1,N_2,\ldots,N_n\) be independent random variables with Poisson distributions and respective parameters \(\lambda_1,\lambda_2,\ldots,\lambda_n\). Then \(N=\sum_{i=1}^nN_i\) follows a Poisson distribution with parameter \(\sum_{i=1}^n\lambda_i\). The probability generating function of \(N\) is the product of the probability generating functions of the \(N_i\): \[ \varphi_N(z)=\prod_{i=1}^n\exp(\lambda_i(z-1)) =\exp\left((z-1)\sum_{i=1}^n\lambda_i\right), \] which makes \(N\) a random variable with a Poisson distribution with parameter \(\sum_{i=1}^n\lambda_i\).
4.6.2 Laplace Transform
4.6.2.1 Definition
Similar to the probability generating function, the Laplace transform does not have an intuitive interpretation. Again, it is a useful tool for obtaining results in risk theory. This function characterizes the distribution of \(X\) and is defined as follows.
Definition 4.5 The Laplace transform of a random variable \(X\), denoted by \(L_X\), is given by \[ L_X(t)=\mathbb{E}[\exp(-tX)],\quad t\geq 0. \]
Laplace transform is often used for non-negative random variables. This ensures its existence and makes it a convenient tool for solving many problems in applied probability.
The moments of \(X\) can be easily obtained by differentiating \(L_X\) and evaluating the derivatives at 0. Specifically, \[ \mathbb{E}[X^k]=(-1)^k\left.\frac{d^k}{dt^k}L_{X}(t)\right|_{t=0}, \quad k\in \mathbb{N}. \]
Table 4.4 presents the Laplace transforms associated with common continuous probability distributions.
| Probability Law | Laplace transform \(L_X(t)\) |
|---|---|
| \(\mathcal{U}ni(a,b)\) | \(\frac{\exp(-at)-\exp(-bt)}{(b-a)t}\) |
| \(\mathcal{B}et(\alpha,\beta)\) | No explicit form |
| \(\mathcal{N}or(\mu,\sigma^2)\) | \(\exp(-\mu t+\frac{1}{2}\sigma^2t^2)\) |
| \(\mathcal{E}xp(\theta)\) | \(\left(1+\frac{t}{\theta}\right)^{-1}\) |
| \(\mathcal{G}am(\alpha,\tau)\) | \(\left(1+\frac{t}{\tau}\right)^{-\alpha}\) |
| \(\mathcal{LN}or(\mu,\sigma^2)\) | No explicit form |
| \(\mathcal{P}ar(\alpha,\theta)\) | No explicit form |
4.6.2.2 Bernstein’s Theorem
Bernstein’s theorem provides a necessary and sufficient condition for a function to be the Laplace transform of a probability distribution. To do this, recall that a function \(g:{\mathbb{R}}^+\to{\mathbb{R}}\) is completely monotone if its derivatives \(g^{(k)}\) of all orders satisfy \[ (-1)^kg^{(k)}(t)\geq 0\mbox{ for all }t>0. \]
Proposition 4.11 (Bernstein's Theorem) A function \(g\) is the Laplace transform of a positive random variable if and only if it is completely monotone and satisfies \(g(0)=1\).
4.6.2.3 Laplace Transform and Convolution
The Laplace transform plays an important role in the analysis of convolutions, as shown by the following result.
Proposition 4.12 Given non-negative and independent random variables \(X_1,X_2,\ldots,X_n\), denoting their sum as \(S=\sum_{i=1}^nX_i\), the Laplace transform \(L_S\) of \(S\) is given by the product of the Laplace transforms \(L_{X_i}\) of each term.
Proof. We can write \[\begin{eqnarray*} L_S(t)&=&\mathbb{E}\left[\exp\left(-t\sum_{i=1}^nX_i\right)\right] \\ &=&\mathbb{E}\left[\prod_{i=1}^n\exp\left(-tX_i\right)\right] \\ &=&\prod_{i=1}^n L_{X_i}(t),\quad t\geq 0. \end{eqnarray*}\]
Thus, under the assumption of independence, we can easily obtain the Laplace transform of the sum of the \(X_i\), while obtaining the corresponding cumulative distribution function is often very difficult.
Example 4.15 (Convolution of Gamma Distributions) The Laplace transform expression of the \(\mathcal{G}am(\alpha,\tau)\) distribution given in Table 4.4 reveals a fundamental property of the gamma distribution: its stability under convolution. Indeed, if \(X_1\) and \(X_2\) are independent random variables with distributions \(\mathcal{G}am(\alpha_1,\tau)\) and \(\mathcal{G}am(\alpha_2,\tau)\) respectively, then \(X_1+X_2\) follows a \(\mathcal{G}am(\alpha_1+\alpha_2,\tau)\) distribution. To see this, notice that the Laplace transform of \(X_1+X_2\) is \[ \left(1+\frac{t}{\tau}\right)^{-\alpha_1} \left(1+\frac{t}{\tau}\right)^{-\alpha_2} =\left(1+\frac{t}{\tau}\right)^{-\alpha_1-\alpha_2} \] which indeed corresponds to the \(\mathcal{G}am(\alpha_1+\alpha_2,\tau)\) distribution.
4.6.2.4 Laplace Transform of Compound Distributions
The following property will be useful, especially in Chapter 9, to approximate compound distributions corresponding to mixed distribution variables (??).
Proposition 4.13 The Laplace transform of \(S\) defined in (??), i.e. \(S=\sum_{i=1}^NX_i\) with \(X_i\), \(i=1,2,\ldots\), independent and identically distributed, and independent of \(N\), is given for \(t>0\) by \(L_S(t)=\varphi_N(L_{X_1}(t))\).
Proof. We can write \[\begin{eqnarray*} L_S(t) & = & \mathbb{E}\left[\exp\left(-t\sum_{i=1}^NX_i\right)\right] \\ & = & \sum_{k=0}^{+\infty}\Pr[N=k]\mathbb{E}\left[\exp\left(-t\sum_{i=1}^kX_i \right)\right] \\ & = & \sum_{k=0}^{+\infty}\Pr[N=k]\{L_{X_1}(t)\}^k = \varphi_N(L_{X_1}(t)). \end{eqnarray*}\]
Example 4.16 As \(\varphi_{N}(z)=\exp\{\lambda(z-1)\}\) when \(N\sim\mathcal{P}oi(\lambda)\), the Laplace transform of \(S\sim\mathcal{CP}oi(\lambda,F_X)\) is \[ L_S(t)=\exp\{\lambda(L_X(t)-1)\},\quad t\in {\mathbb{R}}^+. \]
4.6.2.5 Stability of Compound Poisson Distribution through Convolution
Laplace transforms are quite useful for obtaining results involving convolutions, like the following property.
Proposition 4.14 Consider independent random variables \(S_1\sim\mathcal{CP}oi(\lambda_1,F_1)\), , \(S_n\sim\mathcal{CP}oi(\lambda_n,F_n)\). Then \[ S=\sum_{j=1}^nS_j\sim\mathcal{CP}oi(\lambda_\bullet,F_\bullet), \] where \[ \lambda_\bullet=\sum_{j=1}^n\lambda_j\text{ and }F_\bullet(x)=\frac{1}{\lambda_\bullet} \sum_{j=1}^n\lambda_jF_j(x),\quad x\in\mathbb{R}. \]
Proof. It is enough to write \[ L_S(t)=\prod_{j=1}^nL_{S_j}(t)=\prod_{j=1}^n\exp\{\lambda_j(L_j(t)-1)\}, \] where \(L_j\) is the Laplace transform of the distribution corresponding to the cumulative distribution function \(F_j\). The result is then obtained by noticing that \[ L_s(t)=\exp\{\lambda_\bullet(L_\bullet(t)-1)\}, \] where the Laplace transform \[ L_\bullet(t)=\frac{1}{\lambda_\bullet}\sum_{j=1}^n\lambda_jL_j(t) \] corresponds to the cumulative distribution function \(F_\bullet\).
4.6.2.6 The Case of Infinite Variance Risks
We saw in Property 4.9 that the law of large numbers guarantees (under certain assumptions) the convergence of the average claim amount to the pure premium. However, the reasoning based on (??) assumes that the \(S_i\) have finite variance. The result still holds if the \(S_i\) have infinite variance (which is sometimes the case when the actuary deals with very large claim amounts, invoking the Pareto distribution).
Proposition 4.15 Let \(S_1,S_2,\ldots,S_n\) be non-negative, independent, and identically distributed random variables with finite mean. Then \(\overline{S}^{(n)}\to_{\text{prob}}\mu\) as \(n\to +\infty\).
Proof. Let \(L_S\) be the common Laplace transform of the \(S_i\). The Laplace transform of the sum \(S_1+S_2+\ldots+S_n\) is \(L_S^n\), and that of \(\overline{S}^{(n)}\) is \[ L_{\overline{S}^{(n)}}(t)=\left\{L_S\left(\frac{t}{n}\right)\right\}^n. \] Now, a limited Taylor expansion (to the first order) gives \[ L_S(t)=1-\mu t+o(t), \] where \(o(t)\) is such that \[ \lim_{t\to 0}\frac{o(t)}{t}=0, \] i.e., a function that tends to 0 faster than the identity function (\(o(t)\) is negligible for small values of \(t\)). Therefore, as \(n\to +\infty\) \[\begin{eqnarray*} \lim_{n\to +\infty}L_{\overline{S}^{(n)}}(t)&=&\lim_{n\to +\infty}\left\{L_S\left(\frac{t}{n}\right)\right\}^n\\ &=&\lim_{n\to +\infty}\left\{1-\frac{\mu t}{n}\right\}^n=\exp(-t\mu). \end{eqnarray*}\] Since \(\exp(-t\mu)\) is the Laplace transform associated with the constant \(\mu\), we indeed recover the convergence of \(\overline{S}^{(n)}\) to \(\mu\).
Thus, coverage of risks with infinite variance remains possible. However, intuitively, we can sense that it would be a risky endeavor—it deals with risks for which the spread around the pure premium is infinite!
4.6.3 Moment Generating Function
4.6.3.1 Definition
The moment generating function complements the actuary’s toolkit. It naturally appears in ruin theory and allows for classifying probability distributions according to their associated risks. Unlike the Laplace transform, it is not always defined for non-negative random variables.
Definition 4.6 Given a random variable \(X\), its moment generating function \(M_X\) is defined as \[ M_X(t)=\mathbb{E}[\exp(tX)],\quad t\geq 0. \]
We can see that the difference between the Laplace transform and the moment generating function is essentially formal (\(-t\) is replaced by \(t\)). In actuarial science, it is customary to distinguish between these two tools.
4.6.3.2 Log-Normal Distribution
The moments of the log-normal distribution can be easily obtained from the moment generating function of the normal distribution, as shown in the following example.
Example 4.17 (Moments of the Log-Normal Distribution) When \(X\sim\mathcal{LN}or(\mu,\sigma^2)\), \(X\) has the same distribution as \(\exp(Y)\) where \(Y\sim\mathcal{N}or(\mu,\sigma^2)\). Therefore, \[\begin{eqnarray*} \mathbb{E}[X]=\mathbb{E}[\exp(Y)] & = & M_Y(1)=\exp(\mu+\sigma^2/2), \end{eqnarray*}\] and \[ \mathbb{E}[X^2]=M_Y(2)=\mathbb{E}[\exp(2Y)]=\exp(2\mu+2\sigma^2), \] from which we deduce \[\begin{eqnarray*} \mathbb{V}[X]&=&\exp(2\mu+2\sigma^2)-\exp(2\mu+\sigma^2)\\ &=&\exp(2\mu)\exp(\sigma^2)(\exp(\sigma^2)-1). \end{eqnarray*}\] Thus, the two parameters \(\mu\) and \(\sigma^2\) influence the variability of \(X\).
However, an exponential decay of the tail does not necessarily guarantee the finiteness of the moment generating function. The example of the log-normal distribution illustrates this point. All the moments associated with this distribution exist and are finite. Specifically, if \(X\sim\mathcal{LN}or(\mu,\sigma^2)\), then, generalizing Example 4.17: \[ \mathbb{E}[X^k]=\exp(k\mu+\frac{1}{2}k^2\sigma^2),\quad k=1,2,\ldots \] However, the moment generating function \(M_X(t)\) is always infinite, regardless of the value of \(t\). As a result, the Pareto distribution \(\mathcal{P}ar(\alpha,\theta)\) (for which moments of order \(k>\alpha\) are infinite) does not have a moment generating function.
4.6.3.3 Cramér’s Distribution
In addition to its use in certain mathematical developments, the moment generating function is a convenient tool for assessing the level of risk associated with a distribution used to model the cost of claims. Unlike the Laplace transform, the moment generating function is not necessarily finite. Distributions for which \(M_X\) is constantly infinite indicate a high level of risk for the insurer. The Log-Normal and Pareto distributions fall into this category.
On the contrary, Cramér’s distributions are those for which the moment generating function is finite for at least one positive value of its argument. Such distributions reflect a low or moderate degree of risk for the insurer.
Definition 4.7 The random variable \(X\) has a Cramér distribution if there exists \(h>0\) such that \(M_X(t)\) exists and is finite for \(t<h\).
We obtain by expanding the exponential in a Taylor series: \[ M_X(t)=1+\sum_{k=1}^{+\infty}\frac{t^k}{k!}\mathbb{E}[X^k]\text{ for }t<h. \]
Table 4.5 summarizes the moment generating functions of common continuous probability distributions.
| Probability Law | Moment Generating Function \(M_X(t)\) |
|---|---|
| \(\mathcal{U}ni(a,b)\) | \(\frac{\exp(bt)-\exp(at)}{(b-a)t}\) |
| \(\mathcal{B}et(\alpha,\beta)\) | no explicit form |
| \(\mathcal{N}or(\mu,\sigma^2)\) | \(\exp(\mu t + \frac{1}{2}\sigma^2t^2)\) |
| \(\mathcal{E}xp(\theta)\) | \(\left(1-\frac{t}{\theta}\right)^{-1}\) if \(t<\theta\) |
| \(\mathcal{G}am(\lambda, \alpha)\) | \(\left(1-\frac{t}{\tau}\right)^{-\alpha}\) if \(t<\tau\) |
4.6.3.4 Moment Generating Function and Convolution
Similar to the Laplace transform, the primary interest of the moment generating function lies in the study of sums of random variables. Indeed, the sum of independent random variables amounts to taking the product of the moment generating functions.
Given non-negative independent random variables \(X_1,X_2,\ldots,X_n\), and denoting their sum as \(S=\sum_{i=1}^nX_i\), the moment generating function \(M_S\) of \(S\) is given by the product of the moment generating functions \(M_{X_i}\) of each term.
Proof. It suffices to write \[\begin{eqnarray*} M_S(t)&=&\mathbb{E}\left[\exp\left(t\sum_{i=1}^nX_i\right)\right]\\ &=&\mathbb{E}\left[\prod_{i=1}^n\exp(tX_i)\right]\\ &=&\prod_{i=1}^nM_{X_i}(t). \end{eqnarray*}\]
Example 4.18 (Convolution of Normal Distributions) If \(X\sim\mathcal{N}or(\mu,\sigma^2)\), \[ M_X(t)=\exp(\mu t+\frac{1}{2}t^2\sigma^2). \] This allows us to assert that given independent random variables \(X_i\sim\mathcal{N}or(\mu_i,\sigma_i^2)\), any linear combination \(T=\sum_{i=1}^n\alpha_iX_i\) is also normally distributed. Indeed, the moment generating function of \(T\) is given by \[ \prod_{i=1}^n\mathbb{E}[\exp(\alpha_itX_i)]=\exp\left(\sum_{i=1}^n\alpha_i\mu_i+\frac{t^2}{2}\sum_{i=1}^n\alpha_i^2\sigma_i^2\right), \] which implies that \[ \sum_{i=1}^n\alpha_iX_i\sim\mathcal{N}or\left(\sum_{i=1}^n\alpha_i\mu_i,\sum_{i=1}^n\alpha_i^2\sigma_i^2\right). \]
4.6.3.5 Chernoff Bound
This very useful bound holds for Cramér’s distributions.
Proposition 4.16 Let \(X\) be a random variable with a finite moment generating function, and denote \[ \Psi(t)=\ln M_X(t). \] We have \[ \overline{F}_X(x)\leq\exp(-h(x))\text{ where }h(x)=\sup_{t\geq 0}\{tx-\Psi(t)\}. \]
Proof. The Markov inequality stated in Property ?? gives \[\begin{eqnarray*} \overline{F}_X(x)&=&\Pr[\exp(tX)>\exp(tx)]\\ &\leq&\frac{M_X(t)}{\exp(tx)}=\exp(-(tx-\Psi(t))). \end{eqnarray*}\] Since the above reasoning applies for any \(t>0\), we deduce the announced result from the existence of a moment generating function.
A random variable with a moment generating function must therefore necessarily have a tail function that exponentially decreases to 0.
4.6.4 Hazard Rate
4.6.4.1 Definition
An interesting quantity is the hazard rate (also known as the instantaneous death rate in life insurance), defined as follows.
Definition 4.8 Let \(X\) be a positive random variable with a probability density function \(f_X\). The hazard rate associated with \(X\), denoted as \(r_X\), is given by \[\begin{equation} r_X(x)=-\frac{d}{dx}\ln\overline{F}(x)=\frac{f_X(x)}{\overline{F}_X(x)},\hspace{2mm} x\in {\mathbb{R}}^+.\tag{4.14} \end{equation}\]
4.6.4.2 Interpretation
To better understand the meaning of the hazard rate, it is useful to refer to the following representation of \(r_X\).
Proposition 4.17 The hazard rate can be obtained through the following limit: \[ r_X(x)=\lim_{\Delta x\to 0}\frac{\Pr[x<X\leq x+\Delta x|X>x]} {\Delta x}. \]
Proof. Indeed, \[\begin{eqnarray*} \Pr[x<X\leq x+\Delta x|X>x] & = & \frac{\Pr[x<X\leq x+\Delta x]}{\Pr[X>x]} \\ & = & \frac{\Pr[X>x]-\Pr[X>x+\Delta x]}{\Pr[X>x]}, \end{eqnarray*}\] thus \[\begin{eqnarray*} & & \lim_{\Delta x\to 0}\frac{\Pr[x<X\leq x+\Delta x|X>x]} {\Delta x} \\ & = & \frac{1}{\Pr[X>x]}\lim_{\Delta x\to 0}\frac{\Pr[X>x]-\Pr[X>x+\Delta x]} {\Delta x} \\ & = & -\frac{1}{\Pr[X>x]}\frac{d}{dx}\Pr[X>x] =r_X(x). \end{eqnarray*}\]
In other words, \(r_X(x)\Delta x\) can be interpreted as the probability that the claim amount is approximately equal to \(x\) given that it is at least \(x\). Formally, the hazard rate of a risk \(X\) allows us to approximate the “probability” that \(X\) is equal to \(x\), given that \(X\) exceeds \(x\), i.e. \[ r_X(x)\Delta x\approx \Pr[x<X\leq x+\Delta x|X>x]. \]
Remark. It is interesting to compare this interpretation with the one held by the density function. We have seen in the previous chapter that the density function \(f_X\) of a risk \(X\) evaluated at \(x\) can be interpreted as the “probability” that \(X\) is “equal” to \(x\), since \[ f_X(x)=\lim_{\Delta x\to 0}\frac{\Pr[x<X\leq x+\Delta x]}{\Delta x}, \] so that the approximation \[ f_X(x)\Delta x\approx \Pr[x<X\leq x+\Delta x] \] is valid for sufficiently small \(\Delta x\).
4.6.4.3 Connection with the Tail Function
The following result shows that it is possible to express the tail function of \(x\) in terms of the hazard rate \(r_X\).
Proposition 4.18 The tail function of a positive random variable \(X\) is expressed as follows in terms of the associated hazard rate \(r_X\): \[\begin{equation} \overline{F}(x)=\exp\left(-\int_{\xi=0}^xr_X(\xi)d\xi\right), \hspace{2mm}x\geq 0.\tag{4.15} \end{equation}\]
Proof. It is sufficient to solve the differential equation (4.14) with the initial condition \(\overline{F}(0)=1\).
Property 4.18 shows that the hazard rate \(r_X\) characterizes the probability distribution of \(X\).
4.8 Context
So far, we have assumed that the risks in the portfolio are independent and identically distributed. In most insurances sold to the general public, the dependence between insured risks is not a major issue. In automobile liability insurance, family liability insurance, or theft insurance, it is usually negligible. In fire insurance, it can be easily managed through proper underwriting practices or an appropriate reinsurance program. However, in some cases, the actuary must carefully examine the consequences of dependence; examples include the “earthquake” or “flood” component of fire insurance. The assumption of identical distribution, however, is much less clear. It is clear that certain characteristics of risks influence the probability of a claim occurring or the extent of its consequences.
One of the key features of insurance is that not all individuals are equal in the face of risk: some have a propensity to cause much higher or more frequent claims than others. When these insured parties are mixed in the insurer’s portfolio, it results in some heterogeneity: individuals with a low level of risk coexist with others whose risk level is higher. The insurer can partially address this problem by partitioning the portfolio into more homogeneous risk classes. As we will see later, this is achieved by using observable characteristics of insured parties that significantly influence risk. Even if the portfolio is divided into sub-classes, they often remain very heterogeneous. This heterogeneity of risks covered by the insurer is captured by the mixture models we study in this section.
4.8.1 A Simple Example…
4.8.1.1 A Portfolio with Two Types of Risks
Let’s revisit Example ?? and assume that the risk of loss or theft of luggage varies depending on the traveler’s destination. For countries in group A, let’s say the insurer has to pay the fixed indemnity of 250in 10% of cases, on average, while for countries in group B, the fixed indemnity will be paid in 20% of cases. Thus, for travelers to countries in group A, the insurer’s expense is represented by the random variable \[ S_A=\left\{ \begin{array}{l} 0,\text{ with probability }0.9,\\ 250\text{Euros},\text{ with probability }0.1 \end{array} \right. \] while for a traveler to countries in group B, the expense becomes \[ S_B=\left\{ \begin{array}{l} 0,\text{ with probability }0.8,\\ 250\text{Euros},\text{ with probability }0.2. \end{array} \right. \]
4.8.1.4 Associated Homogeneous Portfolio
In terms of pure premiums, there is no difference between this portfolio and a homogeneous portfolio in which the claim amounts for each policy would follow the distribution \[ S_{AB}=\left\{ \begin{array}{l} 0,\text{ with probability }0.85,\\ 250\text{Euros},\text{ with probability }0.15. \end{array} \right. \] Indeed, the total pure premium income for this homogeneous portfolio is \[ (n_A+n_B)37.5=75n_A. \] Considering the homogeneous portfolio is equivalent to neglecting to differentiate insured parties based on their destination, and thus on the risk they represent(We emphasize that there is no single correct practice. The actuary decides on the model based on the level of solidarity they want to induce in the portfolio. Their goal is not to automatically choose the model that best fits reality. Assuming that the \(S_i\) are independent and identically distributed when they are not amounts to inducing the maximum level of solidarity in the portfolio, which is not necessarily a bad thing). If we acknowledge the heterogeneity of the portfolio, we charge 25or 50based on the destination, while erasing this difference implies applying a uniform premium of 37.5to all insured parties in the portfolio.
4.8.1.5 Consequences of Portfolio Heterogeneity
This simple example introduces several fundamental concepts:
When a uniform premium is charged to insured parties in a heterogeneous portfolio, a certain level of solidarity emerges. Indeed, the 37.5premium paid by an insured traveler to a country in group A can be broken down into a sum of 25, which is the price of their risk, and an additional 12.5, which will artificially lower the premium for travelers to countries in group B. The 25is paid due to risk pooling: it will be used to compensate claims affecting insured parties with the same profile (i.e., traveling to a country in group A). On the other hand, the 12.5reflects the solidarity that the insurer has introduced at the portfolio level by standardizing the premium amount.
When a uniform premium is charged to insured parties in a heterogeneous portfolio, the induced solidarity makes the insurer’s results depend on the portfolio’s structure. For instance, imagine that insured parties traveling to countries in group A are well aware of their risk, realize they are overcharged, and decide not to purchase coverage anymore, deeming the product too expensive. The insurer would then only have insured parties whose destination is a country in group B in the portfolio. Its total pure premium income would amount to \(n_B37.5\text{Euros}\) and would not be sufficient to cover an expected loss of \(n_B50\text{Euros}\). Therefore, the collective premium of 37.5depends on the composition of the portfolio (here, the fact that 50% of trips are to countries in group A). Thus, the pricing is accurate only if the portfolio composition remains the same.
The insurer can hardly maintain a uniform premium in a market where competitors differentiate risks and apply a balanced premium within each defined risk class. In our example, let’s assume that Company \(C_1\), the sole company on the market, charges 37.5to each insured party. A new company \(C_2\) enters the market and differentiates the premium amounts based on the destination country. The insured parties traveling to countries in group A should all switch from \(C_1\) to \(C_2\). The results of \(C_2\) will be balanced, but those of \(C_1\) will deteriorate rapidly, as the insured parties traveling to countries in group A will no longer be there to subsidize the discount granted to insured parties traveling to countries in group B. Company \(C_1\) will have no choice but to raise its uniform premium to 50(if it manages to overcome the loss of \(n_B 12.5\text{Euros}\) it will suffer in the first year when insured parties departing to countries in group A leave). Thus, the market, i.e., Companies \(C_1\) and \(C_2\), will acknowledge the risk difference based on the destination either explicitly (like \(C_2\), which offers a differentiated premium) or implicitly (like \(C_1\), whose pricing structure is such that it only targets a segment of the market).
However, it’s worth mentioning that reality is more subtle. Market players differentiate themselves not only by the premiums they charge but also by the services and extent of coverage they offer, by the target audience they address, and so on. Moreover, insured parties will only decide to switch their insurer if the premium reduction they obtain is substantial enough to justify the effort. The choice of the insurer can also be guided by ideological considerations, as is the case with mutuals.
4.8.1.6 Connection with Mixture Models
The random variable \(S\) representing the claim costs generated by a policy in the portfolio that mixes two types of risks can also be modeled as a mixture of two Bernoulli distributions (scaled by 250). That is, conditional on \(Q=q\), \(S\sim 250\mathcal{B}er(q)\) and \[ Q=\left\{ \begin{array}{l} 0.1,\text{ with probability }\frac{1}{2},\\ 0.2,\text{ with probability }\frac{1}{2}. \end{array} \right. \] Hence, mixture models provide an appropriate tool to handle the heterogeneity of insurance portfolios.
In general, we account for heterogeneity by introducing a random effect \(\Theta\) representing the unknown risk level of the insured party. This results in a mixture model, defined as follows.
Definition 4.11 Suppose that conditional on \(\{\Theta=\theta\}\), the distribution of the random variable \(X\) is described by the cumulative distribution function \(F(\cdot|\theta)\), i.e. \[ \Pr[X\leq x|\Theta=\theta]=F(x|\theta),\hspace{2mm}x\in{\mathbb{R}}. \] If \(\Theta\) is unknown, then the cumulative distribution function of \(X\) is \[ \mathbb{E}\Big[\Pr[X\leq x|\Theta]\Big]=\int_{\theta\in{\mathbb{R}}}F(x|\theta)dF_\Theta(\theta), \] which is a weighted average of the conditional cumulative distribution functions \(F(\cdot|\theta)\) with weights determined by the cumulative distribution function \(F_\Theta\) of \(\Theta\).
4.8.2 Poisson Mixtures
4.8.2.1 Context
Empirically, actuaries have observed that while the Poisson distribution theoretically accounts well for the number of claims caused by each insured party, it poorly models the number of claims affecting a policy in the portfolio. This is primarily due to the heterogeneity of insurance portfolios. If we take the example of auto liability insurance, each insured party has their own driving habits, travel patterns, and operates in an environment dependent on their social and professional activities. As a result, the numbers of claims caused by insured parties in the portfolio will vary more than the Poisson model can capture: indeed, the natural variability of the number of claims associated with the Poisson model is compounded by the variability stemming from portfolio heterogeneity.
Assuming that the number \(N\) of claims caused by an insured party in the portfolio follows the \(\mathcal{P}oi(\lambda)\) distribution implicitly posits that the portfolio is homogeneous: all insured parties have a similar risk profile (captured by the annual claim frequency \(\lambda\)). In practice, this scenario is clearly unlikely: insured parties are not all equal in terms of risk, as explained earlier. The idea is to reflect this portfolio heterogeneity by considering that the average number of claims can vary from one insured party to another: it thus becomes a random variable \(\lambda\Theta\), where \(\Theta\) characterizes deviations around the average number of claims \(\lambda\) (with \(\mathbb{E}[\Theta]=1\)).
4.8.2.2 Definition
This brings us to consider mixtures of Poisson distributions. A mixture distribution reflects the fact that the population of interest results from the mixture of different individuals.
Definition 4.12 The random counting variable \(N\) has a Poisson mixture distribution with mean \(\lambda\) and relative risk level \(\Theta\) when \[\begin{eqnarray} \Pr[N=k]&=&\mathbb{E}\left[\exp(-\lambda\Theta)\frac{(\lambda\Theta)^k}{k!}\right]\nonumber\\ &=&\int_{\theta=0}^{+\infty}\exp(-\lambda\theta)\frac{(\lambda\theta)^k}{k!} dF_\Theta(\theta),\hspace{2mm}k\in {\mathbb{N}},\tag{4.17} \end{eqnarray}\] where \(F_\Theta\) is the cumulative distribution function of \(\Theta\), assumed to satisfy the constraint \(\mathbb{E}[\Theta]=1\). From now on, we will denote \(\mathcal{MP}oi(\lambda,F_\Theta)\) or simply \(\mathcal{MP}oi(\lambda,\Theta)\) as an abuse of notation, the Poisson mixture distribution with mean \(\lambda\) and relative risk level described by \(F_\Theta\); by extension, we will use the same notation for any random variable with distribution (as in (4.17)).
Technically, we want to work with the random pair \((N,\Theta)\); to achieve this, we define its joint probability distribution based on \[ \Pr[\Theta\leq t,N=n]=\int_{\theta=0}^t\exp(-\lambda\theta)\frac{(\lambda\theta)^n}{n!}dF_\Theta(\theta), \] for \(t\in{\mathbb{R}}^+\) and \(n\in{\mathbb{N}}\).
Example 4.19 The simplest model that meets these characteristics is known as the “good risks – bad risks” model. It involves considering that the portfolio consists of two types of risks: good ones, for which the number of claims follows the \(\mathcal{P}oi(\lambda\theta_1)\) distribution, and bad ones, for which the number of claims follows the \(\mathcal{P}oi(\lambda\theta_2)\) distribution, with \(\theta_2>1>\theta_1\). If the proportion of good risks is \(\varrho\), the hypothesis above amounts to \[ \Theta=\left\{ \begin{array}{l} \theta_1,\mbox{ with probability }\varrho, \\ \theta_2,\mbox{ with probability }1-\varrho, \end{array} \right. \] where the parameters \(\theta_1\), \(\theta_2\), and \(\varrho\) are constrained by \[ \mathbb{E}[\Theta]=\varrho\theta_1+(1-\varrho)\theta_2=1. \] The probability that a policy (whose status as a good or bad risk is unknown) results in \(k\) claims during the reference period is then \[ \Pr[N=k]=\varrho\exp(-\lambda\theta_1)\frac{(\lambda\theta_1)^k}{k!}+ (1-\varrho)\exp(-\lambda\theta_2)\frac{(\lambda\theta_2)^k}{k!}, \] by virtue of (4.17).
The above example illustrates the connection between mixing and portfolio heterogeneity. Of course, dividing insured parties into only two categories as in the example above can be simplistic, and multiplying categories inevitably leads to over-parameterization of the model, which goes against the principle of parsimony. Therefore, it is often considered that the risk profile varies continuously in the portfolio (i.e., if insured parties are ranked from worst to best, a continuum is obtained); \(\Theta\) then becomes a continuous random variable with probability density \(f_\Theta\), and \[\begin{equation} \Pr[N=k]=\int_{\theta=0}^{+\infty}\exp(-\lambda\theta)\frac{(\lambda\theta)^k}{k!} f_\Theta(\theta)d\theta,\hspace{2mm}k\in {\mathbb{N}}.\tag{4.18} \end{equation}\]
Remark. On a theoretical level, the insurer facing a number of claims following the \(\mathcal{MP}oi(\lambda,\Theta)\) distribution rather than \(\mathcal{P}oi(\lambda)\) is actually covering a double randomness. It insures not only the uncertainty about the quality of the risk (represented by the unknown claim frequency \(\lambda\Theta\)) but also the uncertainty around the number of claims itself (Poisson randomness).
4.8.2.3 Moments
Let \(N\) be a random variable with \(\mathcal{MP}oi(\lambda,\Theta)\) distribution. The mean of \(N\) is given by \[\begin{eqnarray*} \mathbb{E}[N] & =& \int_{\theta=0}^{+\infty}\left(\sum_{k=0}^{+\infty}k\exp(-\lambda\theta)\frac{(\lambda\theta)^k}{k!}\right) dF_\Theta(\theta)\\ &=&\lambda\int_{\theta=0}^{+\infty}\theta dF_\Theta(\theta)=\lambda. \end{eqnarray*}\] Regarding the variance, it follows that \[\begin{eqnarray*} \mathbb{V}[N]&=& \int_{\theta=0}^{+\infty}\left(\sum_{k=0}^{+\infty}k^2\exp(-\lambda\theta)\frac{(\lambda\theta)^k}{k!}\right) dF_\Theta(\theta)-\lambda^2\\ &=&\int_{\theta=0}^{+\infty}(\lambda\theta+\lambda^2\theta^2) dF_\Theta(\theta)-\lambda^2\\ &=&\lambda+\lambda^2\mathbb{V}[\Theta]. \end{eqnarray*}\] Since \[ \mathbb{V}[N]=\mathbb{E}[N]+\lambda^2\mathbb{V}[\Theta]>\mathbb{E}[N] \] as long as \(\Theta\) is not constant. Thus, any Poisson mixture implies overdispersion of the data.
4.8.2.4 Tail Function
The tail function of \(N\sim\mathcal{MP}oi(\lambda,\Theta)\) can also be expressed as \[\begin{eqnarray*} &&\Pr[N>n]\\ &=&\int_{\theta\in{\mathbb{R}}^+}\sum_{k=n+1}^{+\infty}\exp(-\lambda\theta)\frac{(\lambda\theta)^k}{k!}dF_\Theta(\theta)\\ &=&\int_{\theta\in{\mathbb{R}}^+}\sum_{k=n+1}^{+\infty}\left\{\exp(-\lambda\theta)\frac{\lambda(\lambda\theta)^{k-1}}{(k-1)!} -\exp(-\lambda\theta)\frac{\lambda(\lambda\theta)k}{k!}\right\}\overline{F}_\Theta(\theta)d\theta\\ &=&\lambda\int_{\theta\in{\mathbb{R}}^+}\exp(-\lambda\theta)\frac{(\lambda\theta)^n}{n!}\overline{F}_\Theta(\theta)d\theta. \end{eqnarray*}\]
4.8.2.5 Probability Generating Function
The probability generating function of \(N\sim\mathcal{MP}oi(\lambda,\Theta)\) and the Laplace transform of \(\Theta\) are related by the formula \[\begin{equation} \varphi_N(z)=\int_{\theta=0}^{+\infty}\exp(\lambda\theta(z-1)) f_\Theta(\theta)d\theta=L_\Theta(\lambda(1-z)).\tag{4.19} \end{equation}\]
Example 4.20 (Negative Binomial Distribution) If we consider \(\Theta\sim\mathcal{G}am(a,a)\), then from (4.19) and Table 4.4, we obtain \[ \varphi_{N}(z)=\left(1+\frac{\lambda(1-z)}{\alpha}\right)^{-\alpha}, \] which, according to Table 4.3, is the probability generating function associated with the \(\mathcal{NB}in(\alpha,\alpha/(\alpha+\lambda))\) distribution.
4.8.2.6 Identifiability
Poisson mixtures are identifiable, i.e. if \(N_1\sim\mathcal{MP}oi(\lambda,\Theta_1)\) and \(N_2\sim\mathcal{MP}oi(\lambda,\Theta_2)\) then \[ N_1\stackrel{\text{d}}{=}N_2\Rightarrow \Theta_1\stackrel{\text{d}}{=}\Theta_2. \] Thus, in the context of studying Poisson mixtures, one can reduce it to studying the mixing distributions. This follows from the following reasoning, to which we provide a general scope.
Often when \(N\sim\mathcal{MP}oi(\lambda,\Theta)\), an expectation involving \(N\) can be transformed into an expectation involving \(\Theta\), and vice versa. That is, given a function \(g\), it’s possible to find a function \(g^*\) such that the identity \[ \mathbb{E}[g(\Theta)]=\mathbb{E}[g^*(N)] \] holds. This is the case, for example, when all derivatives \(g^{(1)},g^{(2)},g^{(3)},\ldots\) of \(g\) exist and are positive. In this case, \[ \mathbb{E}[g(\Theta)]= \int_{\theta\in {\mathbb{R}}^+}g(\theta)dF_\Theta(\theta) = \sum_{k=0}^{+\infty}\frac{g^{(k)}(0)}{k!}\int_{\theta\in {\mathbb{R}}^+}\theta^kdF_\Theta(\theta). \] The identity \[ (\lambda\theta)^k=\sum_{\ell=k}^{+\infty}\frac{\exp(-\lambda\theta)(\lambda\theta)^\ell}{(\ell-k)!} \] allows us to write \[\begin{eqnarray*} \mathbb{E}[g(\Theta)] & = & \sum_{k=0}^{+\infty}\frac{g^{(k)}(0)}{\lambda^kk!}\sum_{\ell=k}^{+\infty} \frac{\ell !\Pr[N=\ell]}{(\ell-k)!} \\ & = & \sum_{\ell =0}^{+\infty}\left\{\sum_{k=0}^\ell\binom{\ell}{k}\frac{g^{(k)}(0)}{\lambda^k}\right\} \Pr[N=\ell]\\ &=&\mathbb{E}[g^*(N)] \end{eqnarray*}\] where the function \(g^*\) is defined as \[ g^*(\ell)=\sum_{k=0}^\ell\binom{\ell}{k}\frac{g^{(k)}(0)}{\lambda^k},\hspace{2mm}\ell\in{\mathbb{N}}. \]
Taking \(g(\theta)=\exp(t\theta)\), the associated function \(g^*\) is \[ g^*(\ell)=\sum_{k=0}^\ell\binom{\ell}{k}\frac{t^k}{\lambda^k}=\left(1+\frac{t}{\lambda}\right)^\ell. \] Thus, coming back to the identifiability issue mentioned at the beginning of this section, we have \[\begin{eqnarray*} N_1\stackrel{\text{d}}{=}N_2&\Rightarrow&\mathbb{E}[g^*(N_1)]=\varphi_{N_1}\left(1+\frac{t}{\lambda}\right)\\ &&=\varphi_{N_2}\left(1+\frac{t}{\lambda}\right)=\mathbb{E}[g^*(N_2)]\\ &\Rightarrow&M_{\Theta_1}(t)=\mathbb{E}[g(\Theta_1)]=\mathbb{E}[g(\Theta_2)]=M_{\Theta_2}(t)\\ &\Rightarrow&\Theta_1\stackrel{\text{d}}{=}\Theta_2. \end{eqnarray*}\]
4.8.3 Shaked’s Theorem
Poisson mixtures have a very important property established by (Shaked 1980) known as the “Shaked’s Two Crossings Theorem.”
Proposition 4.22 If \(N\sim\mathcal{MP}oi(\lambda,\Theta)\), then there exist two integer values \(0\leq k_0<k_1\) such that \[\begin{eqnarray*} \Pr[N=k]&\geq& \exp(-\lambda)\frac{\lambda^k}{k!}\text{ for }k=0,1,\ldots,k_0,\\ \Pr[N=k]&\leq& \exp(-\lambda)\frac{\lambda^k}{k!}\text{ for }k=k_0+1,\ldots,k_1,\\ \Pr[N=k]&\geq& \exp(-\lambda)\frac{\lambda^k}{k!}\text{ for }k\geq k_1+1. \end{eqnarray*}\]
Proof. Let’s begin by noting that the number of sign changes in the sequence \[ \Pr[N=k]-\exp(-\lambda)\frac{\lambda^k}{k!},\hspace{2mm}k\in{\mathbb{N}}, \] is the same as the number of sign changes in the sequence \(c(k)\), \(k\in{\mathbb{N}}\), where \[\begin{eqnarray*} c(k)&=&\frac{\Pr[N=k]}{\exp(-\lambda)\frac{\lambda^k}{k!}}-1\\ &=&\int_{\xi\in{\mathbb{R}}^+}\exp(\lambda-\xi)\left(\frac{\xi}{\lambda}\right)^kd\xi-1. \end{eqnarray*}\] Since the function \(c(\cdot)\) is convex, it cannot have more than two sign changes on \({\mathbb{N}}\). Clearly, \(c(\cdot)\) must have at least one sign change. Now, let’s prove that \(c(\cdot)\) cannot have only one sign change. Indeed, in that case, we would have \(\mathbb{E}[N]<\lambda\) or \(\lambda<\mathbb{E}[N]\), which contradicts \(\mathbb{E}[N]=\lambda\).
This result indicates that adding an error \(\Theta\) to the mean \(\lambda\) increases the probability mass assigned to 0: therefore, there will be more policies with no claims in the mixed Poisson model compared to the Poisson model with the same mean. Furthermore, we observe that the probability mass assigned to large values (those exceeding \(k_1+1\)) will be higher in the mixed Poisson model than in the Poisson model with the same mean.
4.8.4 Composite Mixed Poisson Distributions
4.8.4.1 Definition
If \(N\sim\mathcal{MP}oi(\lambda,\Theta)\), then for \(S\) in the form (??), we refer to it as a composite mixed Poisson distribution, denoted as \(S\sim\mathcal{CMP}oi(\lambda,F_\Theta,F)\) or simply \(S\sim\mathcal{CMP}oi(\lambda,\Theta,F)\).
4.8.4.2 Variance
Let’s define the risk index \(r_2\) as \[ r_2=\frac{\mathbb{E}[X_1^2]}{\{\mathbb{E}[X_1]\}^2}. \] Clearly, \(r_2\geq 1\) since \[ r_2-1=\frac{\mathbb{V}[X_1]}{\{\mathbb{E}[X_1]\}^2} \] and \(r_2=1\Leftrightarrow X_1=\) constant. The variance of \(S\sim\mathcal{CMP}oi(\lambda,\Theta,F)\) is then given by \[\begin{eqnarray*} \mathbb{V}[S]&=&\lambda\mathbb{E}[X_1^2]+\lambda^2\{\mathbb{E}[X_1]\}^2\mathbb{V}[\Theta] \\ &=&\{\lambda\mathbb{E}[X_1]\}^2\left({\frac{r_2}{\lambda}+\mathbb{V}[\Theta]}\right). \end{eqnarray*}\] Furthermore, the coefficient of variation of \(S\) is given by \[ CV[S]=\frac{\sqrt{\mathbb{V}[S]}}{\mathbb{E}[S]}=\sqrt{\frac{r_2}{\lambda}+\mathbb{V}[\Theta]}. \] As \[ CV[\mathcal{P}oi(\lambda)]=\sqrt{\frac{r_2}{\lambda}}, \] we observe that when \(\lambda\) is high, \(CV[S]\) is dominated by the behavior of the mixing distribution (expressed by \(\mathbb{V}[\Theta]\)).
The variance of \(S\) can be further decomposed as follows to identify the sources of variability in the insurer’s financial burden: \[\begin{eqnarray*} \mathbb{V}[S]&=&\{\mathbb{E}[X_1]\}^2\mathbb{V}[\mathcal{P}oi(\lambda)]+\lambda\mathbb{V}[X_1]+\lambda^2\{\mathbb{E}[X_1]\}^2\mathbb{V}[\Theta]\\ &\equiv &V_1+V_2+V_3. \end{eqnarray*}\] Let’s give a meaning to each of the three terms in this decomposition:
- the first term \(V_1\) can be seen as \(\mathbb{V}[\mathcal{P}oi(\lambda)\mathbb{E}[X_1]]\), that is, the variance of the insurer’s expense if the claims were constantly equal to their mean and if their number followed a Poisson distribution.
- the second term \(V_2\) can be seen as the contribution of the claim amounts \(X_1,X_2,\ldots\) to the total variability \(\mathbb{V}[S]\), since it is actually \[ \mathbb{V}\left[\sum_{i=1}^\lambda X_i\right], \] ignoring the fact that \(\lambda\) might not be an integer.
- the third and final term \(V_3\) can be considered as the additional variability induced by the mixing distribution.
For small values of \(\lambda\), the variability of the claims predominates, while for large values of \(\lambda\), the effect of the mixing dominates.
4.8.5 Exponential Mixtures
4.8.5.1 Definition
Exponential mixtures constitute a very flexible class of probability distributions. Using an exponential mixture to describe the claim amounts implies considering that the claims follow a negative exponential distribution, but their mean is variable.
Definition 4.14 The continuous random variable \(X\) is said to have an exponential mixture distribution when it has the cumulative distribution function \[\begin{eqnarray} \Pr[X\leq x] & = & \int_{\theta\in {\mathbb{R}}^+} \left\{1-\exp(-\theta x)\right\}dF_\Theta(\theta),\tag{4.21} \end{eqnarray}\] \(x\in {\mathbb{R}}^+\). Hereafter, we will denote by \(\mathcal{ME}xp(F_\Theta)\) or simply \(\mathcal{ME}xp(\Theta)\) the distribution with the cumulative distribution function given by (4.21).
The family of exponential mixtures reflects varying levels of risk for the insurer. If \(\Theta=\theta\), we simply obtain the negative exponential distribution \(\mathcal{E}xp(\theta)\). However, if \(\Theta\) follows a Gamma distribution, we transition to the Pareto distribution, as shown in the following example.
Example 4.21 (Pareto Distribution as an Exponential Mixture) When \(X\sim\mathcal{ME}xp(\Theta)\) and \(\Theta\sim\mathcal{G}am(\alpha,\tau)\), the exponential mixture corresponds to the Pareto distribution. Indeed, the survival function of the exponential mixture is then given by \[\begin{eqnarray*} \Pr[X>x]&=& \frac{\tau^\alpha}{\Gamma(\alpha)}\int_{\theta\in {\mathbb{R}}^+} \exp\left(-\theta(x+\tau)\right)\theta^{\alpha-1} d\theta\\ & = & \frac{1}{\Gamma(\alpha)} \left(\frac{\tau}{x+\tau}\right)^\alpha\int_{\xi\in {\mathbb{R}}^+} \exp(-\xi)\xi^{\alpha-1}d\xi\\ &=&\left(\frac{\tau}{x+\tau}\right)^\alpha, \end{eqnarray*}\] which is indeed the survival function associated with the \(\mathcal{P}ar(\alpha,\tau)\) model.
4.8.5.2 Tail Function
Let’s now examine the tail function associated with an exponential mixture: it’s easy to see that if \(X\sim\mathcal{ME}xp(\Theta)\) then \[\begin{equation} \Pr[X>x]=\int_{\theta\in {\mathbb{R}}^+}\exp(-\theta x)dF_\Theta(\theta) =L_\Theta(x),\hspace{2mm}x\in {\mathbb{R}}^+.\tag{4.22} \end{equation}\] Thus, the tail function of an exponential mixture appears as the Laplace transform of \(\Theta\). This leads us to the following result.
Proposition 4.24 A probability distribution is an exponential mixture if, and only if, its associated tail function is completely monotone.
Proof. As seen earlier, if \(X\sim\mathcal{ME}xp(\Theta)\), the derivatives of the tail function (4.22) can be written as \[\begin{eqnarray*} \frac{d^k}{dx^k}\Pr[X>x] & = & \int_{\theta\in {\mathbb{R}}^+}\left\{\frac{d^k}{dx^k}\exp(-\theta x)\right\} dF_\Theta(\theta)\\ & = & (-1)^k\int_{\theta\in {\mathbb{R}}^+}\theta^{k}\exp(-\theta x)dF_\Theta(\theta), \end{eqnarray*}\] which indeed appears as a completely monotone function. To prove the converse, one just needs to invoke Proposition 4.11.
The Proposition 4.24 notably leads to the fact that the probability density function associated with an exponential model is decreasing and therefore has a unique mode at 0. This might seem restrictive and explains why the model is often used to describe claim amounts exceeding a fixed threshold.
4.8.6 Identifiability of Exponential Mixtures
Note that the uniqueness of the Laplace transform ensures that if \(X\sim\mathcal{ME}xp(\Theta_1)\) and \(Y\sim\mathcal{ME}xp(\Theta_2)\) \[ X=_{\text{law}}Y\Rightarrow\Theta_1=_{\text{law}}\Theta_2, \] making the model identifiable; this allows us to study exponential mixtures through their mixing distribution.
4.8.6.1 Properties
Exponential mixtures enjoy many interesting properties. To establish these, let’s recall the following results about completely monotone functions (see (Feller 1950) for more details).
Lemma 4.1 Let \(g_1\) and \(g_2\) be functions from \((0,+\infty)\) to \([0,+\infty)\).
- If \(g_1\) and \(g_2\) are completely monotone, their product \(g_1g_2\) is also completely monotone.
- If \(g_1\) is completely monotone and \(g_2\) has a completely monotone first derivative, then \(g_1\circ g_2\) is completely monotone. In particular, \(\exp(-g_2)\) is completely monotone. \end{description}
Proposition 4.25 Let \(X_1\sim\mathcal{ME}xp(\Theta_1)\) and \(X_2\sim\mathcal{ME}xp(\Theta_2)\), independently. Then, \[ Z=\min\{X_1,X_2\}\sim\mathcal{ME}xp(\Theta_3)\text{ where }\Theta_3=_{\text{law}}\Theta_1+\Theta_2. \]
Proof. Clearly, \[ \Pr[Z>t]=\Pr[X_1>t]\Pr[X_2>t]; \] thus, the tail function of \(Z\) appears as the product of two completely monotone functions and, by virtue of Lemma 4.1 (1), it is also completely monotone. Proposition 4.24 then allows us to affirm that the distribution of \(Z\) is indeed an exponential mixture. Moreover, \[\begin{eqnarray*} \Pr[Z>t] & = & L_{\Theta_3}(t) \\ & = & \Pr[X_1>t]\Pr[X_2>t] = L_{\Theta_1}(t)L_{\Theta_2}(t), \end{eqnarray*}\] which concludes the proof.
Example 4.22 Consider the family of probability distributions with hazard rate of the form \[ r_X(x)={\theta}+\frac{\alpha}{\lambda+x}, \hspace{2mm}x\in {\mathbb{R}}^+. \] This can be seen as the sum of the hazard rate associated with the negative exponential distribution \(\mathcal{E}xp(\theta)\) and that of the Pareto distribution \(\mathcal{P}ar(\alpha, \lambda)\). As the hazard rate of the random variable \(Z=\min\{X_1,X_2\}\) is the sum of the hazard rates associated with the random variables \(X_1\) and \(X_2\), this family of distributions can be seen as those of the minimum between \(X_1\sim \mathcal{E}xp(\theta)\) and \(X_2\sim\mathcal{P}ar(\alpha, \lambda)\). According to Property 4.25 (1), this family is an exponential mixture with the mixing distribution being the translated Gamma distribution. This model can be used when the estimation of the parameters of the Pareto model yields \(\alpha<2\) (rendering the variance infinite); the Pareto model might be too severe, and this model can be preferred over it.
4.10 Exercises
Exercise 4.1 Establish the following identities: \[\begin{eqnarray*} \mathbb{E}[X] =\mathbb{E}[F_X^{-1}(U)] &=&\int_{p=0}^1F_X^{-1}(p)dp\\ \mathbb{E}[(X-t)_+]&=&\int_{p=F_X(t)}^1F_X^{-1}(p)dp-t\overline{F}_X(t). \end{eqnarray*}\]
Exercise 4.2 To determine the pure premium, we could consider a penalty distance that differentially penalizes underpricing and overpricing, of the form \[ d_*(S,c)=\alpha \mathbb{E}[(S-c)_+]+\beta\mathbb{E}[(c-S)_+]. \] For \(\alpha=\beta\), the average absolute deviation \(d_1\) is obtained up to a factor, and minimizing \(d_*(S,c)\) thus provides the median. If \(\alpha\neq\beta\), show that minimizing \(d_*(S,c)\) leads to the \(\alpha/(\alpha+\beta)\) quantile.
Exercise 4.3 Show that \[ \mathbb{E}[X]=\mathbb{E}[1/r_X(X)]. \]
Exercise 4.4 (IFR and DFR Distributions) When \(r_X\) is decreasing (respectively increasing), \(F\) is called a DFR (respectively IFR) distribution, standing for “Decreasing Failure Rate” (respectively “Increasing Failure Rate”). Clearly, a DFR claim distribution is less favorable for the insurer than an IFR distribution. Prove the following:
- The cumulative distribution function \(F\) of \(X\) is IFR (respectively DFR) if, and only if, the inequality \[ \Pr[X-t_1>x|X>t_1]\geq\mbox{ (respectively} \leq) \Pr[X-t_2>x|X>t_2], \] holds for all \(x\in {\mathbb{R}}^+\), regardless of \(0\leq t_1\leq t_2\).
- The cumulative distribution function \(F\) of \(X\) is IFR (respectively DFR) if, and only if, \[ y\mapsto\frac{\overline{F}(x+y)}{\overline{F}(y)} \] is non-decreasing (respectively non-increasing) for any \(x\), meaning that \(y\mapsto\overline{F}(y)\) is log-convex (respectively log-concave).
Exercise 4.5 (DFR Distributions and Exponential Mixtures) Show that all exponential mixtures are DFR distributions.
Exercise 4.6 (Average Excess of Claims and Tail Function) Assuming that \(e_X(0)=\mathbb{E}[X]<+\infty\), demonstrate that \[ \overline{F}_X(x)=\frac{e_X(0)}{e_X(x)}\exp\left(-\int_{\xi=0}^x\frac{1}{e_X(\xi)}d\xi\right). \]
Exercise 4.7 (IMRL and DMRL Distributions) When \(e_X\) is increasing (respectively decreasing), \(F_X\) is called an IMRL (respectively DMRL) distribution, standing for “Increasing Mean Residual Lifetime” (respectively “Decreasing Mean Residual Lifetime”). Prove the following implications:
- \(F\) is IFR \(\Rightarrow\) \(F\) is DMRL;
- \(F\) is DFR \(\Rightarrow\) \(F\) is IMRL.
Exercise 4.8 Show that a probability distribution whose hazard rate \(r_X\) is completely monotone is a mixture of exponentials.
Exercise 4.9 (Stop-Loss Premium and Variance) Show that for any risks \(X\) and \(Y\) with the same mean \(\mu\), \[\begin{equation} \int_{t=0}^{+\infty}\{\pi_X(t)-\pi_Y(t)\}dt=\frac{1}{2}\{\mathbb{V}[X]-\mathbb{V}[Y]\}. \tag{4.25} \end{equation}\]
Exercise 4.10 Consider claim costs \(X_{0},X_{1},X_{2},\ldots\), assumed to be positive, continuous, independent, identically distributed according to the cumulative distribution function \(F\), and unbounded (i.e., \(F\left( x\right) <1\) for all \(x\)). We want to determine when the next claim with a cost at least as high as \(X_0\) will occur and the amount of this claim: let \(N\) be the first integer such that \(X_{n}>X_{0}\), and then set \(Y=X_{N}\).
- Show that \(\Pr[N=n]=\frac{1}{n(n+1)}\).
- Deduce that \(\mathbb{E}[N]=+\infty\) and interpret this result.
- Show that \[ \Pr[Y<x]=F(x)+\overline{F}(x)\ln\overline{F}(x). \]
Exercise 4.11 A large insurance company covers automobile liability risk. Two factors influence the claim amounts: the vehicle power (low-high) and the driver experience (novice-experienced). It is assumed that the insured population is evenly distributed among these categories (250,000 insured in each category). The average claim amounts according to risk profiles are given in the table below, ??.
- Let’s assume that only two companies, let’s say \(C_1\) and \(C_2\), operate on the market, and that insurance is compulsory. \(C_1\) decides not to differentiate premiums (and charges 1250to all policyholders). The second company \(C_2\) differentiates premiums on the basis of vehicle power. If information is perfect and policyholders systematically opt for the company with the most advantageous rate (meaning, among other things, that the scope of cover offered by \(C_1\) and \(C_2\) is exactly the same), give the average results for \(C_1\) and \(C_2\). How should \(C_1\) react?
- Now let’s assume that \(C_1\) and \(C_2\) apply a segmented tariff according to vehicle power. If a new company \(C_3\) enters the market using driver experience to differentiate policyholders (regardless of vehicle power). How will the three companies fare? What will eventually happen in the market?
| Category | Low.Power | High.Power | All.Vehicles |
|---|---|---|---|
| Experienced | \(100\) | \(900\) | \(500\) |
| Novice | \(1,500\) | \(2,500\) | \(2,000\) |
| All Drivers | \(800\) | \(1,700\) | \(1,250\) |
4.11 Bibliographical notes
The non-life insurance basics presented in this chapter come mainly from (Beard and Pentikäinen 1984), (Borch 1990), (Bühlmann 2007),(Daykin, Pentikainen, and Pesonen 1993), (Gerber 1979), (Kaas et al. 2008), (Pétauton 2000),(Seal 1969), (Straub and Actuaries (Zürich) 1988), (Sundt 1999) and (Tosetti et al. 2000). You can also consult (Booth et al. 2020) for an overview of insurance practice.
Poisson mixtures are presented very clearly in (Grandell 1997).
The formalization of the segmentation concept proposed in Section 4.9.5 is inspired by (De Wit and Van Eeghen 1984).