Chapter 6 Measurement and Comparison of Risks
6.1 Introduction
6.1.1 Measuring Risk: An Essential Task for Actuaries
Measuring risk is undoubtedly one of the most common tasks for actuaries. In fact, it is at the very essence of the profession. Among the measures of risk are, of course, premiums: the amount of the premium must always be proportionate to the risk, thus reflecting the danger associated with the risk transferred to the insurer. Other risk measures attempt to assess the level of economic capital. This is the capital that the company must have in order to be able to compensate for losses. As we saw in Chapter ??, this capital can be determined by limiting the probability of ruin of the insurer to a sufficiently low level. This is the approach based on Value-at-Risk, which we will detail later. We will see that this approach is not without criticism. Indeed, it does not take into account the magnitude of the deficit when ruin occurs. To address this issue, we will turn to tail expectation or Tail Value-at-Risk. This involves determining the capital in a way that can cover the worst scenarios on average.
6.1.2 Comparing Risks: Another Specialty of Actuaries
Throughout history, actuaries have also been concerned with comparing risks. To do this, they have often relied on scalar measures of the inherent danger of a risk \(X\), considering one risk more advantageous than another if the value taken by this measure on this risk is the lowest. Of course, summarizing the entire behavior of a risk in a single scalar measure, no matter how well chosen, often leads to very basic comparisons. This is why actuaries have felt the need to use more sophisticated methods of comparison, some inspired by the expected utility theory of economists (which we will present in a chapter dedicated to economic models of insurance) and others by the simultaneous use of several risk measures.
6.2 Risk Measures
6.2.1 Definition
Let’s start by precisely defining what is meant by a risk measure in this chapter.
Definition 6.1 A risk measure is a functional \(\varrho\) that assigns a positive number, denoted \(\varrho[X]\), possibly infinity, to a risk \(X\).
The idea is that \(\varrho\) quantifies the level of inherent danger of the risk \(X\): large values of \(\varrho[X]\) will indicate that \(X\) is “dangerous” (in a sense to be specified).
Henceforth, we consider \(\varrho[X]\) as the amount of capital that the company must have in order to face a financial loss of amount \(X\). More precisely, as long as \(\varrho\) is normalized, i.e. \[ \varrho[0]=0, \] \(\varrho[X]\) is the minimum amount that, added to the loss \(X\) at the beginning of the period, makes the coverage of \(X\) “acceptable”. The company must therefore have the amount \(\varrho[X]\), which is partly composed of the premiums paid by the insured and, for the rest, by the contribution of capital from the shareholders.
6.2.2 Coherence
It is generally accepted that a risk measure must satisfy certain conditions to be useful in applications. This leads to the notion of a coherent risk measure (artzner1999coherent?).
Definition 6.2 A risk measure is said to be coherent when it possesses the following properties:
- (Axiom 1 (translation invariance)) \(\varrho[X+c]=\varrho[X]+c\) for any risk \(X\) and any constant \(c\). Translation invariance guarantees that \[ \varrho\big[X-\varrho[X]\big]=0. \] Moreover, regardless of the constant \(c\), we should have \[ \varrho[c]=c. \]
- (Axiom 2 (sub-additivity)) \(\varrho[X+Y]\leq \varrho[X]+\varrho[Y]\) for any risks \(X\) and \(Y\). Sub-additivity reflects risk reduction through diversification. The effect of diversification is then measured by \[ \varrho[X]+\varrho[Y]-\varrho[X+Y]\geq 0, \] which represents the capital economy achieved by simultaneously covering risks \(X\) and \(Y\). Additivity is said to occur when there is equality, i.e. \(\varrho[X+Y]=\varrho[X]+\varrho[Y]\) for any risks \(X\) and \(Y\). In this case, the effect of diversification is null.
- (Axiom 3 (homogeneity):) \(\varrho[cX]=c\varrho[X]\) for any risk \(X\) and any positive constant \(c\). Homogeneity is often associated with a certain invariance with respect to monetary units (if we measure financial loss in millions of euros rather than thousands, the risk is not changed and the capital undergoes the same transformation). Homogeneity can also be seen as a limiting case of sub-additivity, when no diversification is possible. Indeed, if we assume that \(c\) is a positive integer, the homogeneity property ensures that \[\begin{eqnarray*} \varrho[cX]&=&\varrho[\underbrace{X+X+\ldots+X}_{c\text{ terms}}]\\ &=&\varrho[X]+\varrho[X]+\ldots+\varrho[X]=c\varrho[X]. \end{eqnarray*}\]
- (Axiom 4 (Monotonicity)) \(\Pr[X\leq Y]=1\Rightarrow\varrho[X]\leq\varrho[Y]\) for any risks \(X\) and \(Y\). This property expresses the fact that more capital is needed when the financial loss becomes more severe. It is therefore very natural. \end{description}
Remark. In the context of risk theory, risk measures must also include a loading for safety, meaning that they must satisfy the inequality \[ \varrho[X]\geq\mathbb{E}[X] \] for any risk \(X\). The minimum capital must exceed the expected loss, otherwise ruin becomes certain (under the conditions of the law of large numbers).
6.2.3 Value-at-Risk
6.2.3.1 Definition
Over the past decade, quantiles have been widely used in risk management, under the now established term Value-at-Risk. The use of this risk measure has been institutionalized by the regulatory authorities in the banking sector in the successive Basel accords.
Definition 6.3 Given a risk \(X\) and a probability level \(\alpha\in(0,1)\), the corresponding VaR, denoted \({\text{VaR}}[X;\alpha]\), is the \(\alpha\) quantile of \(X\). Formally, \[ {\text{VaR}}[X;\alpha]=F_X^{-1}(\alpha). \]
6.2.3.2 VaR is Translation Invariant and Homogeneous
The fact that VaR enjoys these two properties is a direct consequence of the following results, guaranteeing that the VaR of a function \(g\) of the risk \(X\) is obtained by transforming the VaR of \(X\) by the same function.
Lemma 6.1 For any \(p\in (0,1)\),
- if \(g\) is a strictly increasing function and left-continuous, \[ F_{g \left( X\right) }^{-1}\left( p\right) =g \left( F_{X}^{-1}\left( p\right) \right). \]
- if \(g\) is a strictly decreasing function, right-continuous, and if \(F_{X}\) is bijective, \[ F_{g \left( X\right) }^{-1}\left( p\right) =g \left( F_{X}^{-1}\left( 1-p\right) \right). \]
Proof. We only prove (1); the reasoning leading to (2) is analogous. If \(g\) is strictly increasing and left-continuous, then, for any \(0<p<1\), \[\begin{equation*} F_{g \left( X\right) }^{-1}\left( p\right) \leq x\Leftrightarrow p\leq F_{g \left( X\right) }\left( x\right). \end{equation*}\] Since \(g\) is left-continuous, \[ g \left(z\right) \leq x \Leftrightarrow z\leq \sup \left\{ y\in\mathbb{R}|g\left( y\right) \leq x\right\}, \] for any \(x,z\). Thus \[\begin{equation*} p\leq F_{g \left( X\right) }\left( x\right) \Leftrightarrow p\leq F_{X}\left( \sup \left\{ y\in\mathbb{R}|g \left( y\right) \leq x\right\} \right). \end{equation*}\] If \(\sup \left\{ y\in\mathbb{R}|g \left( y\right) \leq x\right\}\) is finite, the desired equivalence is obtained, since \[\begin{equation*} p\leq F_{X}\left( \sup \left\{ y\in\mathbb{R}|g \left( y\right) \leq x\right\} \right) \Leftrightarrow F_{g \left( X\right) }^{-1}\left( p\right) \leq g \left( F_{X}^{-1}\left( p\right) \right), \end{equation*}\] using the fact that \(p\leq F_{X}\left( z\right)\) is equivalent to \(F_{X}^{-1}\left( z\right) \leq z\).
If \(\sup \left\{ y\in\mathbb{R}|g \left( y\right) \leq x\right\}\) is infinite, the above equivalence cannot be used, but the result remains valid. Indeed, if \(\sup \left\{ y\in\mathbb{R}|g \left(y\right) \leq x\right\} =+\infty\), the equivalence becomes \[ p\leq 1\Leftrightarrow F_{X}^{-1}\left( p\right) \leq+\infty. \] The strict increasing of \(g\) and right-continuity allow us to obtain \[\begin{equation*} F_{X}^{-1}\left( p\right) \leq \sup \left\{ y\in\mathbb{R}|g \left( y\right) \leq x\right\} \Leftrightarrow g \left( F_{X}^{-1}\left( p\right) \right) \leq x, \end{equation*}\]% and by combining all inequalities, we can write \[\begin{equation*} F_{g \left( X\right) }^{-1}\left( p\right) \leq x\Leftrightarrow g \left( F_{X}^{-1}\left( p\right) \right)\leq x, \end{equation*}\]% for any \(x\), which implies \(F_{g \left( X\right) }^{-1}\left( p\right) =g \left( F_{X}^{-1}\left( p\right) \right)\) for any \(p\).
Translated into terms of VaR, Lemma 6.1 (1) gives us the following result, showing that VaR is stable under nonlinear increasing transformations.
For any probability level \(\alpha\in(0,1)\) and any increasing and continuous function \(g\), we have that \[ {\text{VaR}}[g(X);\alpha]=g({\text{VaR}}[X;\alpha]). \]
Proof. The cumulative distribution function of the random variable \(g(X)\) is \[ F_{g(X)}(t) = \Pr[g(X) \leq t] = \Pr[X \leq g^{-1}(t)] = F_X(g^{-1}(t)). \] Hence, \[\begin{eqnarray*} {\text{VaR}}[g(X);1-\alpha] &=& \inf\{t \in \mathbb{R} \mid F_{g(X)}(t) \geq 1-\alpha\} \\ &=& \inf\{t \in \mathbb{R} \mid F_X(g^{-1}(t)) \geq 1-\alpha\} \\ &=& \inf\{t \in \mathbb{R} \mid g^{-1}(t) \geq {\text{VaR}}[X;1-\alpha]\} \\ &=& \inf\{t \in \mathbb{R} \mid t \geq g({\text{VaR}}[X;1-\alpha])\} \\ &=& g({\text{VaR}}[X;1-\alpha]), \end{eqnarray*}\] which completes the proof.
By taking \(g(x) = x+c\) and \(g(x) = cx\), it is immediately deduced from this latter property that VaR is invariant under translation and homogeneous.
6.2.3.3 VaR is not subadditive
The following example illustrates that the VaR of a sum can exceed the sum of the VaRs associated with each of the terms. Thus, the diversification effect is not always positive with VaR, and this risk measure does not consistently favor diversification.
Example 6.1 Consider the independent risks \(X \sim \mathcal{P}ar(1,1)\) and \(Y \sim \mathcal{P}ar(1,1)\), i.e. \[ \Pr[X > t] = \Pr[Y > t] = \frac{1}{1+t}, \quad t > 0. \] Then we have \[ {\text{VaR}}[X;\alpha] = {\text{VaR}}[Y;\alpha] = \frac{1}{1-\alpha} - 1. \] Moreover, it can be verified that \[ \Pr[X+Y \leq t] = 1 - \frac{2}{2+t} + 2\frac{\ln(1+t)}{(2+t)^2}, \quad t > 0. \] Since \[ \Pr\big[X+Y \leq 2{\text{VaR}}[X;\alpha]\big] = \alpha - \frac{(1-\alpha)^2}{2}\ln\left(\frac{1+\alpha}{1-\alpha}\right) < \alpha, \] the inequality \[ {\text{VaR}}[X;\alpha] + {\text{VaR}}[Y;\alpha] < {\text{VaR}}[X+Y;\alpha] \] holds for any \(\alpha\), showing that VaR cannot be subadditive in this case.
6.2.5 Esscher Risk Measure
6.2.5.1 Definition
The Esscher risk measure consists of taking the pure premium of the Esscher transform of the initial risk, formalized as follows.
Definition 6.8 The Esscher risk measure with parameter \(h>0\) of the risk \(X\), denoted as \({\text{Es}}[X;h]\), is given by \[ {\text{Es}}[X;h] = \frac{\mathbb{E}[X\exp(hX)]}{M_X(h)} = \frac{d}{dh}\ln M_X(h). \]
Remark. In fact, \({\text{Es}}[X;h]\) is none other than the expected value of the Esscher transform \(X_h\) of \(X\), whose cumulative distribution function is given by (??), i.e. \[ {\text{Es}}[X;h] = \mathbb{E}[X_h] = \int_{\xi\in{\mathbb{R}}^+}\xi \, dF_{X,h}(\xi). \] So, the initial risk \(X\) is replaced by a less favorable risk \(X_h\) before calculating the pure premium.
6.2.5.2 Esscher Risk Measure Contains Safety Loading
The Esscher risk measure is increasing in the parameter \(h\), as shown by the following result.
\({\text{Es}}[X;h]\) is an increasing function of \(h\).
Proof. The announced result follows directly from \[\begin{eqnarray} \frac{d}{dh}\mathbb{E}[X_h] &=&\int_{\xi\in{\mathbb{R}}^+}x^2 \, dF_{X,h}(\xi) - \left(\int_{\xi\in{\mathbb{R}}^+}x \, dF_{X,h}(\xi)\right)^2 \nonumber\\ &=&\mathbb{V}[X_h]\geq 0.\tag{6.5} \end{eqnarray}\]
This property ensures that for any \(h>0\), \[ {\text{Es}}[X;h]\geq{\text{Es}}[X;0]=\mathbb{E}[X], \] so the Esscher risk measure contains a safety loading.
6.2.5.3 Incoherence of the Esscher Risk Measure
The Esscher risk measure is not homogeneous (except in the trivial case \(h=0\)). It is invariant under translation but not monotonic, as shown by the following example.
Example 6.2 Consider the risks \(X\) and \(Y\) defined as \[\begin{eqnarray*} \Pr[X=0,Y=0]&=&\frac{1}{3},\\ \Pr[X=0,Y=3]&=&\frac{1}{3},\\ \Pr[X=6,Y=6]&=&\frac{1}{3}. \end{eqnarray*}\] In this case, \(\Pr[X\leq Y]=1\), but \[ {\text{Es}}[X;1/2]=5.4567>{\text{Es}}[Y;1/2]=5.2395. \]
6.2.6 Wang Risk Measures
6.2.6.1 Definition
These risk measures exploit the representation of the mathematical expectation established in Property ??. The idea is to transform the tail function in order to generate a safety loading. We will now call any non-decreasing function $g:$ with \(g(0)=0\) and \(g(1)=1\) a distortion function.
Definition 6.9 The Wang risk measure associated with the distortion function \(g\), denoted as $_{g}$, is defined as \[\begin{equation} \rho _{g}\left[ X\right] =\int_{0}^{\infty }g\left( \overline{F}_{X}(x)\right) \, dx. \tag{6.6} \end{equation}\]
Remark. In light of this definition, the following comments can be made:
- The distortion function \(g(q)=q\) corresponds to the mathematical expectation $$.
- Clearly, if \(g(q)\geq q\) for all $q$, then \(\rho _{g}\left[ X\right] \geq \mathbb{E}\left[ X\right]\), indicating that Wang risk measures associated with such distortion functions contain a safety loading.
- Moreover, it is interesting to note that if \(g_{1}(q)\leq g_{2}(q)\) for all $q$, then ${g{1}}{g{2}}$.
6.2.6.2 Wang Risk Measures and VaR
By substituting \(\int_0^{\overline{F}_X(x)}dg(\alpha)\) for \(g\left( \overline{F}_{X}(x)\right)\) in (6.6) and interchanging the integrals, we obtain the following result.
Proposition 6.2 For any risk \(X\), the Wang risk measure associated with the distortion function \(g\) can be written as \[\begin{equation} \rho _{g}\left[ X\right] =\int_{0}^{1}{\text{VaR}}[X;1-\alpha]\ dg(\alpha)\text{.} \tag{6.7} \end{equation}\]
Thus, Wang risk measures are mixtures of VaR. In particular, if we consider the distortion function \(g:[0,1]\to [0,1]\) defined as \[ g_\alpha(x)=\mathbb{I}[x\geq 1-\alpha] \] for a fixed value of \(\alpha\in [0,1)\), then by (6.7) we have \[ \rho_{g_\alpha}[X]={\text{VaR}}[X;\alpha] \] which shows that the VaR at probability level \(\alpha\) is a particular Wang risk measure corresponding to a distortion function that increases from 0 to 1 at \(1-\alpha\).
Remark. In this case, \(g_\alpha\) is a cumulative distribution function corresponding to the constant \(1-\alpha\).
6.2.6.3 Wang Risk Measures and TVaR
Similarly, starting from (6.7) with the distortion function \[ g_\alpha(x)=\min\left\{\frac{x}{1-\alpha},1\right\}, \] for a fixed \(\alpha\in[0,1]\) we obtain \[ \rho_{g_\alpha}[X]=\frac{1}{1-\alpha}\int_0^{1-\alpha}{\text{VaR}}[X;1-\xi]d\xi={\text{TVaR}}[X;\alpha]. \]
Remark. In this case as well, \(g_\alpha\) is a cumulative distribution function corresponding to the uniform distribution \(\mathcal{U}ni(0,1-\alpha)\).
6.2.6.4 ES is Not a Wang Risk Measure
Let’s assume for a contradiction that \({\text{ES}}[X;\alpha]\) can indeed be represented as a Wang risk measure associated with a distortion function \(g_\alpha\), i.e. \({\text{ES}}[X;\alpha]=\rho_{g_\alpha}[X]\) for any risk \(X\). Take \(X\sim\mathcal{U}ni (0,1)\). In this case, \[\begin{eqnarray} {\text{ES}}[X;\alpha]&=&\int_\alpha^1(1-x)dx\nonumber\\ &=&\frac{1}{2}(1-\alpha)^{2}\nonumber\\ &=&\rho_{g_\alpha}[X]=\int_{0}^{1}g_\alpha(1-x)dx. \tag{6.8} \end{eqnarray}\] Now, consider \(Y\sim\mathcal{B}er(q)\) for \(0<q\leq 1-\alpha\). It’s easy to see that \[ {\text{ES}}[Y;\alpha]=q=\rho_{g_\alpha}[Y]=g_\alpha(q) \] which implies \(g_\alpha(q)=q\) for \(0<q\leq 1-\alpha\). Inserting this into (6.8) gives us \[\begin{eqnarray*} \frac{1}{2}(1-\alpha)^{2}&\geq &\frac{1}{2} (1-\alpha)^{2}+\alpha(1-\alpha), \end{eqnarray*}\] which leads to a contradiction since \(0<\alpha<1\).
6.2.6.5 CTE is Not a Wang Risk Measure
We can formally establish by contradiction that CTE is not a Wang risk measure either. We can proceed similarly to how we did for ES. Assume for a contradiction that there exists a distortion function \(g_\alpha\) such that \({\text{CTE}}[X;\alpha]=\rho_{g_\alpha}[X]\) for any risk \(X\). For \(X\sim\mathcal{U}ni(0,1)\), we have from (6.3) \[\begin{equation*} {\text{CTE}}[X;\alpha]=\alpha+\frac{1}{2}(1-\alpha)=\int_{0}^{1}g_\alpha\left( 1-x\right) dx, \end{equation*}\] which simplifies to \[\begin{equation} \int_{0}^{1}g_\alpha\left( x\right) dx=\frac{1}{2}(1+\alpha). \tag{6.9} \end{equation}\] Now, consider \(Y\sim\mathcal{B}er(q)\) for \(0<q\leq 1-\alpha\). We get \({\text{CTE}}[Y;\alpha]=1\). Therefore, \[ g_\alpha(q)=\rho_{g_\alpha}[Y]={\text{CTE}}[Y;\alpha]=1 \] which implies that \(g_\alpha(\cdot )\equiv 1\) on \((0,1]\), contradicting equation (6.9) and proving that CTE is not a Wang risk measure.
6.2.6.6 Dual Power Risk Measure
Taking \[ g(x)=1-(1-x)^\xi, \hspace{2mm}\xi\geq 1, \] we get \[ \rho_g[X]=\int_{x\geq 0}(1-\{F_X(x)\}^\xi)dx. \] If \(\xi\) is an integer, \(\rho_g[X]\) can be interpreted as the expected value of the maximum \(M_\xi=\max\{X_1,\ldots,X_\xi\}\) of a set of \(\xi\) independent and identically distributed random variables with the same distribution as \(X\). Indeed, the tail distribution function of \(M_\xi\) is given by \[ \Pr[M_\xi>x]=1-\Pr[X_1\leq x,\ldots,X_\xi\leq x]=1-\{F_X(x)\}^\xi, \] so \(\rho_g[X]=\mathbb{E}[M_\xi]\).
6.2.6.7 PH Risk Measure
Consider the distortion function \[ g(x)=x^{1/\xi},\hspace{2mm}\xi\geq 1. \] The PH risk measure is given by \[ \text{PH}_\xi[X]=\rho_g[X]=\int_{x\geq 0}\{\overline{F}_X(x)\}^{1/\xi}dx. \] Note that for \(\xi=1\), \(\text{PH}_1[X]=\mathbb{E}[X]\).
6.2.6.8 Comparison of Major Distortion Functions
The curves in Figure 6.1 show the shapes of the major distortion functions, where \(p\) is a constant between \(0\) and \(1\)., including:
| Name | Mathematical function |
|---|---|
| VaR | \(g(x) = \mathbb{I}[x \geq p]\) |
| Tail-VaR | \(g(x) = \min \{x/p, 1\}\) |
| PH | \(g(x) = x^{p}\) |
| Dual Power | \(g(x) = 1 - (1 - x)^{1/p}\) |
| Gini | \(g(x) = (1 + p)x - px^{2}\) |
| Exponential Transformation | \(g(x) = \frac{1 - p^{x}}{1 - p}\) |
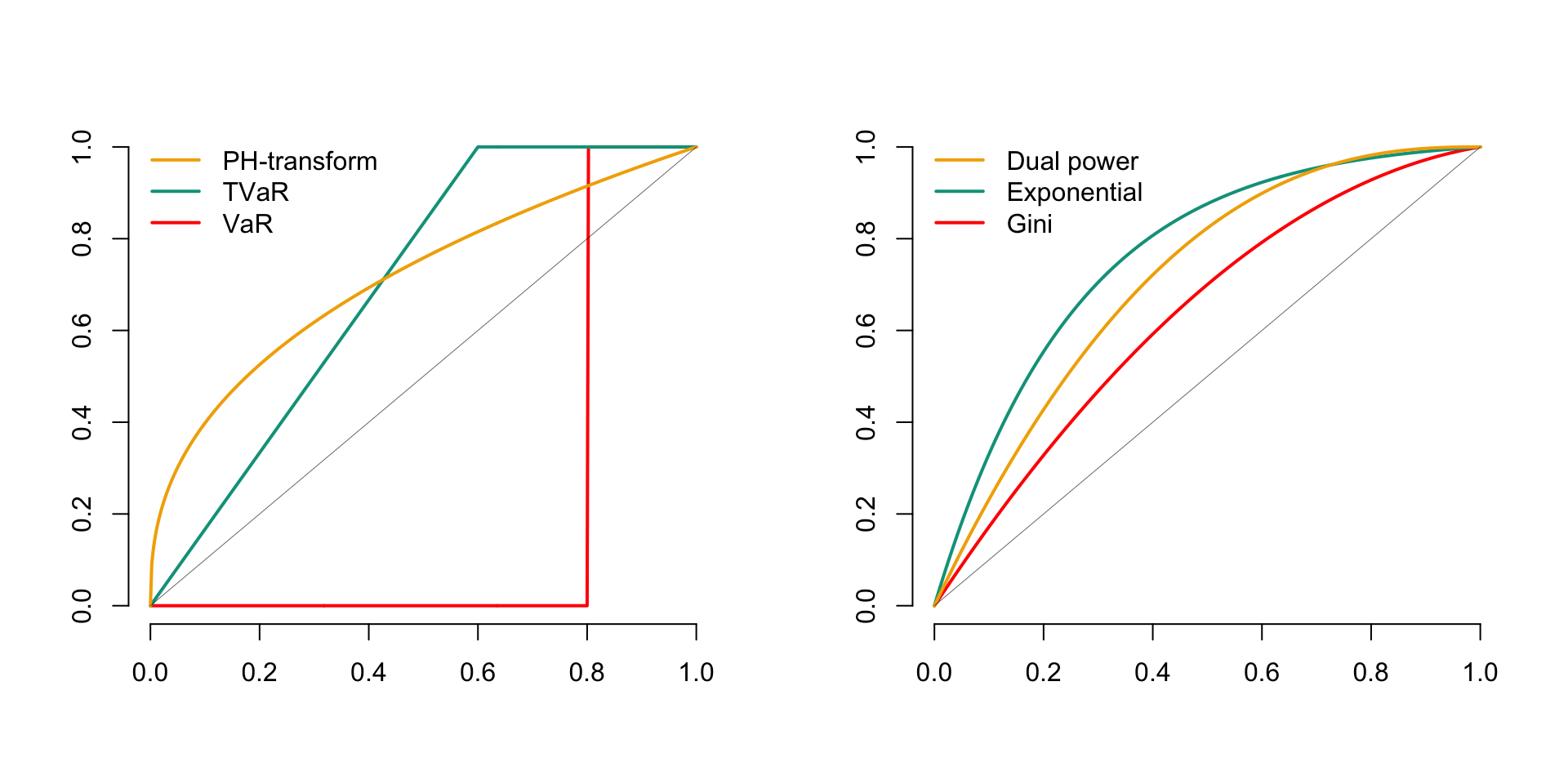
Figure 6.1: Major Distortion Functions
Remark. We will delve more deeply into different distortion functions in insurance microeconomics in Volume 2.
6.3 Main Properties of Wang’s Risk Measures
The main properties of Wang’s risk measures are summarized in the following result.
Proposition 6.3
- The risk measures of Wang are homogeneous.
- The risk measures of Wang are translation invariant.
- The risk measures of Wang are monotonic.
Proof. Working from Property 6.2, and considering the fact that VaR is translation invariant, we obtain \[\begin{eqnarray*} \rho _{g}\left[ X+c\right] &=&\int_{0}^{1}\text{VaR}[X+c;1-\alpha]\ dg(\alpha)\\ &=&\int_{0}^{1}\big(\text{VaR}[X;1-\alpha]+c\big)\ dg(\alpha)\\ &=&\rho_g[X]+c\big(g(1)-g(0)\big)=\rho_g[X]. \end{eqnarray*}\] This establishes (i). Similarly, we deduce the homogeneity and monotonicity of Wang’s measures from the corresponding properties of VaR.
6.3.1 Concavity of the Distortion Function
If the distortion function \(g\) is concave, the function \(x\mapsto g(\overline{F}_{X}(x))\) is right-continuous and is thus the tail function of a certain random variable. In this situation, \(\rho_{g}\left[ X\right]\) is indeed a mathematical expectation (not of \(X\) but of a variable \(Y\) with tail function \(\overline{F}_Y(y)=g(\overline{F}_{X}(y))\)). The following result illustrates the significance of the concavity assumption on \(g\).
When the distortion function is concave, the corresponding risk measure is subadditive.
6.4 Uniform Comparison of VaR
6.4.1 Definition
We have extensively studied the properties of VaR. Given two risks \(X\) and \(Y\), it is natural to compare them using the VaR corresponding to a level \(\alpha_1\), i.e., consider \(X\) to be less risky than \(Y\) if \(\text{VaR}[X;\alpha_1] \leq \text{VaR}[X;\alpha_1]\). However, often the choice of probability level is not immediately apparent, and it is possible to have simultaneously \[ \text{VaR}[X;\alpha_1] \leq \text{VaR}[X;\alpha_1] \] and \[ \text{VaR}[X;\alpha_2] \geq \text{VaR}[X;\alpha_2] \] for two probability levels \(\alpha_1\) and \(\alpha_2\). In such a situation, which of the risks, \(X\) or \(Y\), is less risky?
To avoid these difficulties, we will adopt the following definition, which suggests comparing the risks \(X\) and \(Y\) by requiring that the VaRs relative to these risks are ordered for any choice of the probability level.
Definition 6.10 Given two risks \(X\) and \(Y\), we will consider \(X\) less risky than \(Y\) based on VaR comparison, denoted as \(X\preceq_{\text{VaR}}Y\), when \[ \text{VaR}[X;\alpha] \leq \text{VaR}[Y;\alpha] \text{ for all } \alpha \in (0,1). \]
The relation \(\preceq_{\text{VaR}}\) that we have defined constitutes a partial order on the set of probability distributions (it can be easily verified to be reflexive, antisymmetric, and transitive). However, it is not antisymmetric with respect to random variables. Indeed, \(X\preceq_{\text{VaR}}Y\) and \(Y\preceq_{\text{VaR}}X\) do not imply \(X=Y\), but only \(X=_{\text{law}}Y\).
The relation \(\preceq_{\text{VaR}}\) has been studied extensively in probability and statistics (for example, see (Lehmann 1955)). It is better known in these fields as the stochastic order or distribution order. Economists and actuaries have also made significant use of it, under the name of first-order stochastic dominance. Other common notations for \(\preceq_{\text{VaR}}\) include \(\preceq_{st}\), \(\preceq_1\), or \(\preceq_{FSD}\).
6.4.2 Equivalent Conditions
We establish several equivalent conditions for having \(\preceq_{\text{VaR}}\) between two risks \(X\) and \(Y\). The first of these informs us that it is equivalent to compare VaRs or distribution functions (with the latter being the inverses of VaRs).
For two random variables \(X\) and \(Y\), \[\begin{eqnarray*} X\preceq_{\text{VaR}}Y &\Leftrightarrow& F_X(t)\geq F_Y(t) \text{ for all } t \in \mathbb{R},\\ &\Leftrightarrow& \overline{F}_X(t) \leq \overline{F}_Y(t) \text{ for all } t \in \mathbb{R}. \end{eqnarray*}\]
Interpreting \(\overline{F}_X(t)\) as the probability that \(X\) takes a “large” value (i.e., a value greater than \(t\)), this property shows that \(X\preceq_{\text{VaR}}Y\) means that \(X\) is “smaller” than \(Y\), since the probability that \(X\) takes large values is always less than that of \(Y\) taking large values.
Remark (Insensitivity of $\lst$ to Variance). The relation \(\preceq_{\text{VaR}}\) does not provide any information about the variances of the compared random variables. For example, if we take \(X\sim\text{Bernoulli}(p)\) and \(Y=1\), we have \(X\preceq_{\text{VaR}}Y\) even though \[ \text{Var}[X]=p(1-p)>\text{Var}[Y]=0. \] This demonstrates that \(\preceq_{\text{VaR}}\) focuses on comparing the magnitude of risks rather than their variability.
The stochastic order \(X\preceq_{\text{VaR}}Y\) allows us to derive numerous interesting inequalities, as demonstrated by the following result.
For two random variables \(X\) and \(Y\), \[ X\preceq_{\text{VaR}}Y \Leftrightarrow \mathbb{E}[g(X)] \leq \mathbb{E}[g(Y)] \text{ for all increasing functions } g, \] provided the expectations exist.
Proof. It suffices to recall that if \(U \sim \text{Uniform}(0,1)\), then \(X \stackrel{\text{d}}{=} \text{VaR}[X;U]\) according to Property ??. With this result in mind, we have the following representation, valid for any function \(g\): \[ \mathbb{E}[g(X)] = \mathbb{E}\left[g\left(\text{VaR}[X;U]\right)\right] = \int_0^1 g\left(\text{VaR}[X;u]\right)du. \] The stated result is then obtained simply by writing \[\begin{eqnarray*} \mathbb{E}[g(X)] &=& \int_0^1 g\left(\text{VaR}[X;u]\right)du \\ &\leq& \int_0^1 g\left(\text{VaR}[Y;u]\right)du = \mathbb{E}[g(Y)]. \end{eqnarray*}\]
In addition to the above results, we now demonstrate that we can restrict ourselves to regular functions \(g\) in Property ??.
Proposition 6.4 For two random variables \(X\) and \(Y\), \(X\preceq_{\text{VaR}}Y \Leftrightarrow \mathbb{E}[g(X)] \leq \mathbb{E}[g(Y)]\) for any function \(g\) such that \(g' \geq 0\), provided the expectations exist.
Proof. The implication ” \(\Rightarrow\) ” is evident. To prove the converse, note that \[ \mathbb{I}[x>t] = \lim_{\sigma\to 0}\Phi\left(\frac{x-t}{\sigma}\right). \] Furthermore, the function \(x \mapsto -\Phi\left(\frac{t-x}{\sigma}\right)\) is increasing. Therefore, we have in particular \[ -\mathbb{E}\left[\Phi\left(\frac{t-Y}{\sigma}\right)\right] \leq -\mathbb{E}\left[\Phi\left(\frac{t-X}{\sigma}\right)\right], \] which yields \[\begin{eqnarray*} \Pr[X>\text{Norm}(t,\sigma)] &=& \mathbb{E}\left[\Phi\left(\frac{X-t}{\sigma}\right)\right] \\ &\leq & \mathbb{E}\left[\Phi\left(\frac{Y-t}{\sigma}\right)\right] \\ &=& \Pr[Y>\text{Norm}(t,\sigma)] \end{eqnarray*}\] for any \(\sigma>0\). This same inequality holds when taking the limit as \(\sigma\to 0\), resulting in \(\Pr[X>t] \leq \Pr[Y>t]\). Since this reasoning holds for any \(t\), this concludes the proof.
6.4.2.1 Sufficient Conditions
Property ?? informs us that risks \(X\) and \(Y\) satisfy \(X\preceq_{\text{VaR}}Y\) when their respective tail functions mutually dominate each other. The following result provides a sufficient condition for this to hold. It suffices that the probability density functions only cross once.
Proposition 6.5 For any risks \(X\) and \(Y\), if \(f_X(t) \geq f_Y(t)\) for \(t<c\) and \(f_X(t) \leq f_Y(t)\) for \(t>c\), then \(X\preceq_{\text{VaR}}Y\).
Proof. It suffices to observe that if \(x<c\), \[ F_X(x) = \int_0^x f_X(t)dt \geq \int_0^x f_Y(t)dt = F_Y(x) \] and if \(x>c\), \[ \overline{F}_X(x) = \int_x^{+\infty} f_X(t)dt \geq \int_x^{+\infty} f_Y(t)dt = \overline{F}_Y(x). \] Thus, we have \(X\preceq_{\text{VaR}}Y\) under the conditions stated above, which completes the proof.
6.4.3 Properties
6.4.3.1 Stability of \(\preceq_{\text{VaR}}\) with respect to standard deductible clauses
The developments in this paragraph are based on the following result.
Proposition 6.6 For any random variables \(X\) and \(Y\), \[ X\preceq_{\text{VaR}}Y \Rightarrow t(X)\preceq_{\text{VaR}}t(Y) \] for any non-decreasing function \(t\).
Proof. The result is immediately deduced from the following observation: for any non-decreasing function \(g\), the function \(x\mapsto g(t(x))\) is non-decreasing when \(t\) is non-decreasing.
Property 6.6 guarantees, among other things, that when \(X\preceq_{\text{VaR}}Y\), \[\begin{eqnarray*} (X-\delta)_+ & \preceq_{\text{VaR}}&(Y-\delta)_+\text{ for any deductible }\delta\in{\mathbb{R}},\\ &&\text{mandatory underwriting,}\\ \alpha X & \preceq_{\text{VaR}}&\alpha Y\text{ for any }\alpha>0,\\ X\mathbb{I}[X>\kappa] & \preceq_{\text{VaR}}&Y\mathbb{I}[Y>\kappa]\text{ for any threshold }\kappa\in{\mathbb{R}},\\ \min\{X,\omega\} & \preceq_{\text{VaR}}&\min\{Y,\omega\}\text{ for any cap }\omega\in{\mathbb{R}}. \end{eqnarray*}\] This implies that a comparison in the \(\preceq_{\text{VaR}}\) sense is not affected by the introduction of a standard deductible clause related to damages (whether it’s a mandatory underwriting, a deductible, or an upper limit) in the policy terms.
6.4.3.2 Stability of \(\preceq_{\text{VaR}}\) in the Presence of Uncertainty
Regardless of the risks \(X\) and \(Y\) and the random vector \(\boldsymbol{\Theta}\), if \(X\preceq_{\text{VaR}}Y\) when \(\boldsymbol{\Theta}=\boldsymbol{\theta}\), then the stochastic inequality remains valid when \(\boldsymbol{\Theta}\) is unknown. Indeed, as \[ \Pr[X\leq x|\boldsymbol{\Theta}=\boldsymbol{\theta}]\geq \Pr[Y\leq x|\boldsymbol{\Theta}=\boldsymbol{\theta}] \text{ for all }\boldsymbol{\theta}\text{ and }x, \] we easily deduce that \[\begin{eqnarray*} \Pr[X\leq x] & = & \int_{\boldsymbol{\theta}}\Pr[X\leq x|\boldsymbol{\Theta}=\boldsymbol{\theta}] dF_{\boldsymbol{\Theta}}(\boldsymbol{\theta})\\ & \geq & \int_{\boldsymbol{\theta}} \Pr[Y\leq x|\boldsymbol{\Theta}=\boldsymbol{\theta}] dF_{\boldsymbol{\Theta}}(\boldsymbol{\theta})=\Pr[Y\leq x], \end{eqnarray*}\] which proves the announced result.
6.4.4 Hazard Rate and PH Risk Measure
6.4.4.1 Definition and Equivalent Conditions
We could be interested in comparing risks given that they exceed a certain level \(t\). Thus, we could require that \[ [X|X>t]\preceq_{\text{VaR}}[Y|Y>t] \] for any level \(t\). The following example shows that this is not necessarily true when \(X\preceq_{\text{VaR}}Y\).
Example 6.3 Show that \[\begin{equation*} X\preceq_{\text{VaR}}Y\nRightarrow [X|X>t] \preceq_{\text{VaR}}[Y|Y>t] \text{ for any }t. \end{equation*}\] Consider, for instance, the case where \(X\sim \mathcal{U}ni(0,3)\) and \(Y\) has the density \[ f_{Y}\left( x\right) =\frac{1}{6} \mathbb{I}_{\left] 0,1\right] }\left( x\right)+\frac{1}{2}\mathbb{I}_{\left] 1,2\right] }\left( x\right)+ \frac{1}{3}\mathbb{I}_{\left] 2,3\right[ }\left(x\right). \] Then, \(X\preceq_{\text{VaR}}Y\), but \([X|X>1]\sim\mathcal{U}ni(1,3)\) and \([Y|Y>1]\) has the density \[ f_{Y}^{\ast }\left( x\right) =\frac{3}{5}\mathbb{I}_{\left] 1,2\right] }\left( x\right)+\frac{2}{5}\mathbb{I}_{\left] 2,3\right[ }\left(x\right) \] so that \[ [Y|Y>1]\preceq_{\text{VaR}}[X|X>1]. \]
We can prove the following result.
Proposition 6.7 Given two risks \(X\) and \(Y\), \([X|X>t]\preceq_{\text{VaR}}[Y|Y>t]\) for any \(t\in{\mathbb{R}}\) if, and only if \[\begin{eqnarray*} &\Leftrightarrow & t\mapsto \frac{\overline{F}_Y(t)}{\overline{F}_X(t)}\text{ is non-decreasing}(\#eq:eq1.B.3b)\\ &\Leftrightarrow & \overline{F}_X(u)\overline{F}_Y(v)\ge\overline{F}_X(v)\overline{F}_Y(u)\quad \text{for any}\quad u\le v.(\#eq:eq1.B.4) \end{eqnarray*}\]
This comparison can be related to the hazard rates, as shown in the following result.
Given two risks \(X\) and \(Y\), \([X|X>t]\preceq_{\text{VaR}}[Y|Y>t]\) for any \(t\in{\mathbb{R}}\) if, and only if \(r_X(t)\geq r_Y(t)\) for any \(t\).
Proof. The ratio \(\overline{F}_Y/\overline{F}_X\) is non-decreasing if, and only if, \(\ln \overline{F}_Y/\overline{F}_X\) is also non-decreasing. This further implies that \(\ln \overline{F}_Y-\ln\overline{F}_X\) is non-decreasing, which is equivalent to \(r_X-r_Y>0\) since, according to Property ??, \[ \frac{d}{dt}\Big\{\ln\overline{F}_Y(t)-\ln\overline{F}_X(t)\Big\}=r_X(t)-r_Y(t). \]
6.4.4.2 Hazard Rate and PH Risk Measure
Let’s suppose we deflate the hazard rate by a factor \(\xi\), i.e., we transition from a rate \(r_X\) to a rate \(r_{X^*}\) given by \[ r_{X^*}(t)=\frac{r_X(t)}{\xi}\leq r_X(t),\text{ for }\xi\geq 1. \] Using Property ??, we obtain a tail function \[ \overline{F}_{X^*}(t)=\exp\left(-\int_0^t\frac{r_X(s)}{\xi}ds\right)=\{\overline{F}_X(t)\}^{1/\xi}. \] Therefore, PH\([X;\xi]=\mathbb{E}[X^*]\). The PH risk measure consists of replacing the original risk \(X\) with a transformed risk \(X^*\) whose hazard rate has been deflated, and then calculating the expectation associated with \(X^*\). We have \[ [X|X>t]\preceq_{\text{VaR}}[X^*|X^*>t]\text{ for any }t>0. \]
6.4.5 Likelihood Ratio and Esscher Principle
6.4.5.1 Definition
We could also consider imposing \[ [X|a\leq X\leq a+h]\preceq_{\text{VaR}}[Y|a\leq Y\leq a+h] \] for any level \(a\) and increment \(h>0\). This corresponds to the situation of a reinsurer who would cover the interval \((a,a+h]\) of a risk \(X\), i.e., who would expose themselves to a loss of \[ X_{(a,a+h]}= \left\{ \begin{array}{l} 0\text{ if }X<a\\ X-a\text{ if }a\leq X<a+h\\ h\text{ if }a+h\leq X, \end{array} \right. \] where \(a\) is the retention and \(h\) is the limit.
We can establish the following result.
(#prp:Propo5.4.10) Consider the random variables \(X\) and \(Y\), both continuous or discrete, with probability density functions \(f_X\) and \(f_Y\). If \[\begin{equation} \frac{f_X(t)}{f_Y(t)}\quad\text{decreases over the union of the supports of $X$ and $Y$} (\#eq:eq1.C.1) \end{equation}\] (taking \(a/0\) as \(+\infty\) when \(a>0\) by convention), or equivalently, if \[\begin{equation} f_X(u)f_Y(v)\ge f_X(v)f_Y(u)\quad\text{for all}\quad u\le v, (\#eq:eq1.C.2) \end{equation}\] then \([X|a\leq X\leq a+h]\preceq_{\text{VaR}}[Y|a\leq Y\leq a+h]\) for any level \(a\) and increment \(h>0\).
Proof. Consider \(a<b\). The stochastic inequality \([X|a\leq X\leq b]\preceq_{\text{VaR}}[Y|a\leq Y\leq b]\) guarantees that \[ \frac{\Pr[u\le X\le b]}{\Pr[a\le X\le b]}\le\frac{\Pr[u\le Y\le b]} {\Pr[a\le Y\le b]}\quad\text{when}\quad u\in[a,b]. \] This implies \[ \frac{\Pr[a\le X<u]}{\Pr[u\le X\le b]}\ge\frac{\Pr[a\le Y<u]} {\Pr[u\le Y\le b]}\quad\text{when}\quad u\in [a,b]. \] In other words, \[ \frac{\Pr[a\le X<u]}{\Pr[a\le Y<u]}\ge\frac{\Pr[u\le X\le b]} {\Pr[u\le Y\le b]}\quad\text{when}\quad u\in [a,b]. \] Particularly, for \(u<b\le v\), \[ \frac{\Pr[u\le X<b]}{\Pr[u\le Y<b]}\ge\frac{\Pr[b\le X\le v]} {\Pr[b\le Y\le v]}. \] Hence, when \(X\) and \(Y\) are continuous, \[ \frac{\Pr[a\le X<u]}{\Pr[a\le Y<u]}\ge\frac{\Pr[b\le X\le v]} {\Pr[b\le Y\le v]}\quad\text{when}\quad a<u\le b\le v. \] Taking limits as \(a\rightarrow u\) and \(b\rightarrow v\), we obtain @ref(eq:eq1.C.2). The proof in the discrete case is similar.
The conditions @ref(eq:eq1.C.1) and @ref(eq:eq1.C.2), seemingly technical and not very intuitive, are generally easy to establish in parametric models.
Remark. The method of comparing probability distributions discussed in Proposition @ref(prp:Propo5.4.10) is also called the likelihood ratio order and denoted by \(\preceq_{lr}\).
6.4.5.2 Connection with the Esscher Transform
Let \(X_h\) be the Esscher transform of \(X\). The ratio of the probability densities associated with \(X\) and \(X_h\) is proportional to \(\exp(-hx)\), which is clearly decreasing in \(x\). This indicates that \[ [X|a\leq X\leq b]\preceq_{\text{VaR}}[X_h|a\leq X_h\leq b], \] for any \(a<b\).
The following result shows under which conditions the Esscher risk measures relative to two risks \(X\) and \(Y\) are uniformly ordered.
Proposition 6.8 If \([X|a\leq X\leq b]\preceq_{\text{VaR}}[Y|a\leq Y\leq b]\) for any \(a<b\), then \({\text{Es}}[X;h]\leq{\text{Es}}[Y;h]\) for any \(h>0\).
Proof. Due to Proposition @ref(prp:Propo5.4.10), we know that the inequality \[ f_X(u)f_Y(v)\geq f_X(v)f_Y(u) \] holds for any \(u\leq v\). By multiplying both sides of this inequality by \[ \frac{\exp(hu)}{M_X(h)} \frac{\exp(hv)}{M_Y(h)} \] we obtain the same inequality for the probability density functions of \(X_h\) and \(Y_h\), from which we conclude that \([X_h|a\leq X_h\leq b]\preceq_{\text{VaR}}[Y_h|a\leq Y_h\leq b]\), giving the desired result.
6.5 Uniform Comparison of TVaRs
6.5.1 Definition
Here, we introduce a new method of comparing risks based on Tail Value-at-Risk (TVaR).
Definition 6.11 For any random variables \(X\) and \(Y\) with finite mean, \(X\) will be considered less risky than \(Y\) based on the comparison of TVaRs, denoted as \(X\preceq_{\text{TVaR}}Y\), when \[ {\text{TVaR}}[X;\alpha]\leq{\text{TVaR}}[Y;\alpha]\text{ for all }\alpha\in[0,1]. \]
The restriction to risks with finite mean ensures the existence of TVaRs, and thus the correctness of the definition of \(\preceq_{\text{TVaR}}\). Therefore, we now only compare risks with finite pure premium (it’s worth noting that many results we will establish in the following section depend on this assumption). This distinction also sets apart \(\preceq_{\text{VaR}}\) and \(\preceq_{\text{TVaR}}\): indeed, \(\preceq_{\text{VaR}}\) is defined for any variables in consideration, whereas this is not the case for \(\preceq_{\text{TVaR}}\).
The \(\preceq_{\text{TVaR}}\) relation is quite old (it’s a direct descendant of the relation known as “majorization” among numerical vectors, studied in the 1930s). Actuaries still refer to it as the stop-loss order (denoted \(\preceq_{sl}\)), a concept closely related to the second-order stochastic dominance (often denoted as \(\preceq_2\) or \(\preceq_{SSD}\)) in economics. Probability theorists are more familiar with the \(\preceq_{\text{TVaR}}\) relation under the name of increasing convex order (denoted \(\preceq_{icx}\)).
We will also use the relation denoted \(\preceq_{\text{TVaR,=}}\), which restricts \(\preceq_{\text{TVaR}}\) to pairs of random variables with the same mean.
Definition 6.12 For any random variables \(X\) and \(Y\), \[\begin{eqnarray*} X\preceq_{\text{TVaR,=}}Y&\Leftrightarrow& \left\{ \begin{array}{l} \mathbb{E}[X]=\mathbb{E}[Y],\\ X\preceq_{\text{TVaR}}Y, \end{array} \right. \\ &\Leftrightarrow& \left\{ \begin{array}{l} {\text{TVaR}}[X;0]={\text{TVaR}}[Y;0],\\ {\text{TVaR}}[X;\alpha]\leq{\text{TVaR}}[Y;\alpha]\\ \hspace{20mm}\text{for all }\alpha\in(0,1). \end{array} \right. \end{eqnarray*}\]
The \(\preceq_{\text{TVaR,=}}\) relation is known as the convex order among probability theorists (denoted \(\preceq_{cx}\)). It is closely related to other relations, such as the Lorenz order.
Remark. Note that \(\preceq_{\text{VaR}}\) did not allow the comparison of random variables with the same mean. Indeed, for any risks \(X\) and \(Y\), \[ \left. \begin{array}{l} X\preceq_{\text{VaR}}Y\\ \mathbb{E}[X]=\mathbb{E}[Y] \end{array} \right\} \Rightarrow X=_{\text{law}} Y. \] To prove this result, it suffices to examine the identity \[ \mathbb{E}[Y]-\mathbb{E}[X]=\int_{x=0}^{+\infty} \underbrace{\{\Pr[Y>x]-\Pr[X>x]\}}_{\geq 0 \text{ for all }x}dx=0, \] which implies \(\Pr[Y>x]=\Pr[X>x]\) for all \(x\) and concludes the verification.
6.9 Bibliographical notes
The coherent risk measures, whose applications in actuarial science were emphasized by (artzner1999coherent?) are detailed in (Denuit et al. 2006). Also see (Tasche 2002). The risk measures by Shaun Wang are studied notably in (Wang 1996) and (Wang 1998).
This chapter prominently features stochastic orders. From a general perspective, a stochastic order refers to any method of comparing probability distributions (of random variables, random vectors, stochastic processes, etc.), meaning any binary relation defined on a set of probability distributions. Among the stochastic orders between real-valued random variables, there are relations that can be defined with reference to a class of measurable functions. These orders, also known as integral orders, often have a natural interpretation in the framework of expected utility theory. Examples include the distribution order, convex and concave orders, convex-increasing and concave-increasing orders, and the exponential order.
Readers interested in stochastic orders will find a general introduction in (shaked1994stochastic?), which also provides numerous applications in various fields. For a more advanced probabilistic analysis, consider (Szekli 2012), and for applications in economics, refer to (Levy 1992). Applications of stochastic orders in insurance are described in (Goovaerts et al. 1990), as well as in (Kaas, Van Heerwaarden, and Goovaerts 1994) and (Gouriéroux 1999). For a more theoretical approach, explore (Müller and Stoyan 2002).